题目内容
已知：函数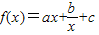
（a、b、c是常数）是奇函数，且满足
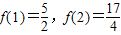，（Ⅰ）求a、b、c的值；
（Ⅱ）试判断函数f（x）在区间
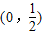上的单调性并证明．
【答案】分析：（1）由函数是奇函数得到c=0，再利用题中的2个等式求出a、b的值．
（2）区间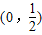
上任取2个自变量x1、x2，将对应的函数值作差、变形到因式积的形式，判断符号，
依据单调性的定义做出结论．
解答：解：（1）∵f（-x）=-f（x）∴c=0∵
∴
∴
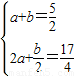（2）∵由（1）问可得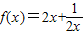
∴
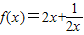在区间（0，0.5）上是单调递减的
证明：设任意的两个实数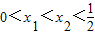
∵
=
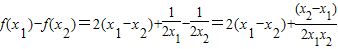
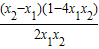
又∵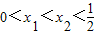
∴x1-x2＜0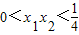
，1-4x1x2＞0f（x1）-f（x2）＞0
∴
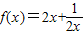在区间（0，0.5）上是单调递减的．
点评：本题考查用待定系数法求解析式，证明函数的单调性．
（2）区间
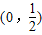上任取2个自变量x1、x2，将对应的函数值作差、变形到因式积的形式，判断符号，依据单调性的定义做出结论．
解答：解：（1）∵f（-x）=-f（x）∴c=0∵
∴
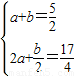∴（2）∵由（1）问可得
∴
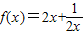
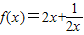在区间（0，0.5）上是单调递减的证明：设任意的两个实数
∵
=
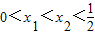
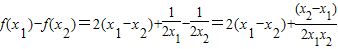
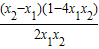
又∵
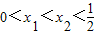
∴x1-x2＜0
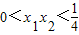，1-4x1x2＞0f（x1）-f（x2）＞0∴
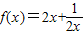在区间（0，0.5）上是单调递减的．点评：本题考查用待定系数法求解析式，证明函数的单调性．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
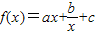（a、b、c是常数）是奇函数，且满足
，
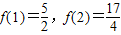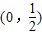上的单调性并证明．
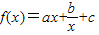（a、b、c是常数）是奇函数，且满足
，
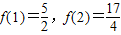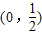上的单调性并证明．
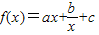（a、b、c是常数）是奇函数，且满足
，
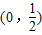上的单调性并证明．
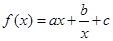（a、b、c是常数）是奇函数，且满足
．
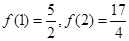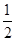)上的单调性并证明．