网址:http://m.1010jiajiao.com/timu_id_559096[举报]
一、选择题(本大题共8小题,每小题5分,共40分)
1.A 2.A 3.B 4.B 5.C 6.D 7.B 8.B
二、填空题(本大题共6小题,每小题5分,共30分)
9.- 10.5 11.2,
10.5 11.2, 12.12 13.26 14.-
12.12 13.26 14.-
注:两个空的填空题第一个空填对得2分,第二个空填对得3分.
三、解答题(本大题共6小题,共80分)
15.(本小题满分13分)
(Ⅰ)解:f(x)=cos2x-sin2x+2 sinxcosx+1=
sinxcosx+1= sin2x+cos2x+1
sin2x+cos2x+1
=2sin +1. ……………………………………………5分
+1. ……………………………………………5分
因此f(x)的最小正周期为 ,最小值为-1.……………………………7分
,最小值为-1.……………………………7分
(Ⅱ)由f( )=2得2 sin
)=2得2 sin +1=2,即sin
+1=2,即sin =
= . ………9分
. ………9分
而由 ∈
∈ 得2
得2 +
+ ∈
∈ .……………………………10分
.……………………………10分
故2 +
+ =
= .…………………………………………………………12分
.…………………………………………………………12分
解得 =
= . ………………………………………………………………13分
. ………………………………………………………………13分
16.(本小题满分13分)
解:(Ⅰ)要得40分,8道选择题必须全做对,在其余四道题中,有两道题答对的概率为 ,有一道题答对的概率为
,有一道题答对的概率为 ,还有一道题答对的概率为
,还有一道题答对的概率为 ,所以得40分的概率为
,所以得40分的概率为
P= ×
× ×
× ×
× =
= . ………………………………………………5分
. ………………………………………………5分
(Ⅱ)依题意,该考生得分 的取值是20,25,30,35,40,得分为20表示只做对了四道题,其余各题都做错,故求概率为P(
的取值是20,25,30,35,40,得分为20表示只做对了四道题,其余各题都做错,故求概率为P( =20)=
=20)= ×
× ×
× ×
× =
= ;
;
同样可求得得分为25分的概率为
P( =25)=
=25)= ×
× ×
× ×
× ×
× +
+ ×
× ×
× ×
× +
+ ×
× ×
× ×
× =
= ;
;
得分为30分的概率为P( =30)=
=30)= ;
;
得分为35分的概率为,P( =35)=
=35)= ;
;
得分为40分的概率为P( =40)=
=40)= .
.
于是 的分布列为
的分布列为

20
25
30
35
40
P





………………………………………………………………………………11分
故E =20×
=20× +25×
+25× +30×
+30× +35×
+35× +40×
+40× =
= .
.
该考生所得分数的数学期望为 ………………………………………13分
………………………………………13分
17.(本小题满分14分)
解法一:
 (Ⅰ)在直三棱柱ABC-A1B1C1中,CC1
(Ⅰ)在直三棱柱ABC-A1B1C1中,CC1 底面
底面
ABC,BC1在底面上的射影为CB.
由AC=3,BC=4,AB=5,可得AC CB.
CB.
所以AC BC1………………………4分
BC1………………………4分
(Ⅱ)过C作CE AB于E,连结C1E.
AB于E,连结C1E.
由CC1 底面ABC可得C1E
底面ABC可得C1E AB.
AB.
故∠CEC1为二面角C1-AB-C的平面角.
在 ABC中,CE=
ABC中,CE= ,
,
在Rt CC1E中,tanC1EC=
CC1E中,tanC1EC= =
= ,
,
故所求二面角的大小为arctan .……9分
.……9分
(Ⅲ)存在点D使AC1∥平面CDB1,且D为AB中点,下面给出证明.
设BC1与CB1交于点O,则O为BC1中点.连接OD.
在△ABC1中,D,O分别为AB,BC1的中点,故OD为△ABC1的中位线,
∴OD∥AC1,又AC1 平面CDB1,OD
平面CDB1,OD 平面CDB1,
平面CDB1,
∴AC1∥平面CDB1.
故存在点D为AB中点,使AC1∥平面CDB1. ………………………………14分
解法二:
∵直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴AC,BC,CC1两两垂直.如图以C为坐标原点,建立空间直角坐标系C-xyz,则
C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4).
(Ⅰ)∵ =(-3,0,0),
=(-3,0,0), =(0,-4,4),
=(0,-4,4),
∴ ?
? =0,故AC
=0,故AC BC1 ………………………………………………4分
BC1 ………………………………………………4分
 (Ⅱ)平面ABC的一个法向量为m=(0,0,1),设平面C1AB的一个法向量为
n=(x0,y0,z0),
(Ⅱ)平面ABC的一个法向量为m=(0,0,1),设平面C1AB的一个法向量为
n=(x0,y0,z0),
 =(-3,0,4),
=(-3,0,4), =(-3,4,0).
=(-3,4,0).
由 得
得
令x0=4,则z0=3,y0=3.
则n=(4,3,3).
故cos<m,n>= =
= .
.
所求二面角的大小为arccos . ………………………………………9分
. ………………………………………9分
(Ⅲ)同解法一 ………………………………………………………………………4分
18.(本小题满分13分)
解:(Ⅰ)依题意有,f ′(x)=a+ .……………………………………………3分
.……………………………………………3分
因此过(1,f(1))点的直线的斜率为a-1,又f(1)=a,
所以,过(1,f(1))点的直线方程为y-a=(a-1)(x-1).…………4分
又已知圆的圆心为(-1,0),半径为1,依题意, =1.
=1.
解得a=1. …………………………………………………………………6分
(Ⅱ)f ′(x)=a+ .
.
因为a>0,所以2- <2,又由已知x<2.………………………………9分
<2,又由已知x<2.………………………………9分
令f ′(x)>0,解得x<2- ,令f ′(x)<0,解得2-
,令f ′(x)<0,解得2- <x<2. …11分
<x<2. …11分
所以,f(x)的单调增区间是 ,
,
f(x)的单调减区间是 .………………………………………13分
.………………………………………13分
19.(本小题满分13分)
解:(Ⅰ)由已知抛物线的焦点为(0,- ),故设椭圆方程为
),故设椭圆方程为 +
+ =1.
=1.
将点A(1, )代入方程得
)代入方程得 +
+ =1,整理得a4-5a2+4=0,
=1,整理得a4-5a2+4=0,
解得a2=4或a2=1(舍).
故所求椭圆方程为 +
+ =1. …………………………………………6分
=1. …………………………………………6分
(Ⅱ)设直线BC的方程为y= x+m,设B(x1,y1),C(x2,y2),
x+m,设B(x1,y1),C(x2,y2),
代入椭圆方程并化简得4x2+2 mx+m2-4=0, …………………………9分
mx+m2-4=0, …………………………9分
由 =8m2-16(m2-4)=8(8-m2)>0,可得m2<8.
=8m2-16(m2-4)=8(8-m2)>0,可得m2<8.
由x1+x2=- m,x1x2=
m,x1x2= ,
,
故 =
= =
= .
.
又点A到BC的距离为d= , …………………………………………11分
, …………………………………………11分
故 =
=
 ?d=
?d= ≤
≤ ?
? =
= ,
,
当且仅当2m2=16-2m2,即m=±2时取等号(满足 >0)
>0)
所以△ABC面积的最大值为 . ………………………………………13分
. ………………………………………13分
20.(本小题满分14分)
解:(Ⅰ)依题意有yn= +
+ ,于是yn+1-yn=
,于是yn+1-yn= .
.
所以数列 是等差数列. ………………………………………………4分
是等差数列. ………………………………………………4分
(Ⅱ)由题意得 =n,即xn+xn+1=2n,(n∈N*)①
=n,即xn+xn+1=2n,(n∈N*)①
所以又有xn+2+ xn+1=2(n+1). ②……………………6分
由②-①得xn+2-xn=2,可知x1,x3,x5,…;x2,x4,x6,…都是等差数列.那么得
x2k-1=x1+2(k-1)=2k+a-2,
x2k=x2+2(k-1)=2-a+2(k-1)=2k-a.(k∈N*)
故xn= ……………………………………………10分
……………………………………………10分
(Ⅲ)当n为奇数时,An(n+a-1,0),An+1(n+1-a,0),所以 =2(1-a);
=2(1-a);
当n为偶数时,An(n-a,0)An+1(n+a,0),所以 =2a;
=2a;
作BnCn x轴,垂足为Cn,则
x轴,垂足为Cn,则 =
= +
+ ,要使等腰三角形AnBnAn+1为直角三角形,必须且只需
,要使等腰三角形AnBnAn+1为直角三角形,必须且只需 =2
=2 .
.
当n为奇数时,有2(1-a)=2 ,即12a=11-3n. ①
,即12a=11-3n. ①
当n=1时,a= ;当n=3时,a=
;当n=3时,a= ;当n≥5时,①式无解.
;当n≥5时,①式无解.
当n为偶数时,有12a=3n+1,同理可求得a= .
.
综上所述,上述等腰三角形AnBnAn+1中存在直角三角形,此时a的值为 或
或 或
或 . ………………………………………………………………………14分
. ………………………………………………………………………14分
| 2 |
| 2 |
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知直线l的方向向量为(1,
| 2 |
| 2 |
| 2 |
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知直线l的斜率是
| 2 |
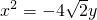 的焦点是椭圆M的一个焦点,又点A
的焦点是椭圆M的一个焦点,又点A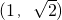 在椭圆M上.
在椭圆M上.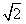 y的焦点是椭圆M的一个焦点,又点A(1,
y的焦点是椭圆M的一个焦点,又点A(1,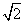 )在椭圆M上。
)在椭圆M上。 的直线
的直线 与椭圆M交于B、C两点,求△ABC面积的最大值。
与椭圆M交于B、C两点,求△ABC面积的最大值。