题目内容
已知椭圆M的对称轴为坐标轴,且抛物线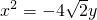 的焦点是椭圆M的一个焦点,又点A
的焦点是椭圆M的一个焦点,又点A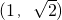 在椭圆M上.
在椭圆M上.
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知直线l的方向向量为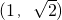 ,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.
,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.
解:(Ⅰ)由已知抛物线的焦点为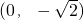 ,故设椭圆方程为
,故设椭圆方程为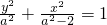 .
.
将点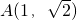 代入方程得
代入方程得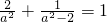 ,整理得a4-5a2+4=0,
,整理得a4-5a2+4=0,
解得a2=4或a2=1(舍).
故所求椭圆方程为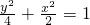 .(6分)
.(6分)
(Ⅱ)设直线BC的方程为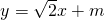 ,设B(x1,y1),C(x2,y2),
,设B(x1,y1),C(x2,y2),
代入椭圆方程并化简得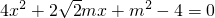 ,
,
由△=8m2-16(m2-4)=8(8-m2)>0,可得m2<8.(*)
由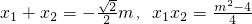 ,
,
故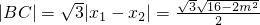 .
.
又点A到BC的距离为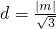 ,
,
故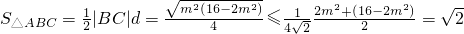 ,
,
当且仅当2m2=16-2m2,即m=±2时取等号(满足*式)
所以△ABC面积的最大值为 .(12分)
.(12分)
分析:(Ⅰ)先求出抛物线的焦点坐标,进而设出椭圆方程,再把点A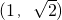 代入方程求出a,即可求椭圆M的方程;
代入方程求出a,即可求椭圆M的方程;
(Ⅱ)先利用直线l的方向向量为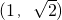 ,求出直线的斜率,设出直线方程;再与椭圆方程联立,求出B、C两点的坐标与m的关系;再求出B、C两点之间的线段长以及点A到BC的距离,代入△ABC面积的表达式,再结合不等式的有关知识求出△ABC面积的最大值即可.
,求出直线的斜率,设出直线方程;再与椭圆方程联立,求出B、C两点的坐标与m的关系;再求出B、C两点之间的线段长以及点A到BC的距离,代入△ABC面积的表达式,再结合不等式的有关知识求出△ABC面积的最大值即可.
点评:本题主要考查直线与圆锥曲线的综合问题.第一问涉及到了求抛物线的焦点坐标,在求抛物线的焦点坐标时,一定注意先把抛物线方程转化为标准形式,再求解,避免出错.
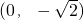 ,故设椭圆方程为
,故设椭圆方程为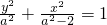 .
.将点
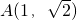 代入方程得
代入方程得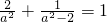 ,整理得a4-5a2+4=0,
,整理得a4-5a2+4=0,解得a2=4或a2=1(舍).
故所求椭圆方程为
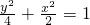 .(6分)
.(6分)(Ⅱ)设直线BC的方程为
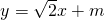 ,设B(x1,y1),C(x2,y2),
,设B(x1,y1),C(x2,y2),代入椭圆方程并化简得
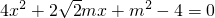 ,
,由△=8m2-16(m2-4)=8(8-m2)>0,可得m2<8.(*)
由
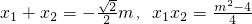 ,
,故
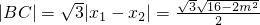 .
.又点A到BC的距离为
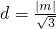 ,
,故
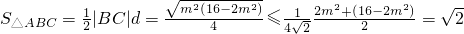 ,
,当且仅当2m2=16-2m2,即m=±2时取等号(满足*式)
所以△ABC面积的最大值为
 .(12分)
.(12分)分析:(Ⅰ)先求出抛物线的焦点坐标,进而设出椭圆方程,再把点A
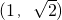 代入方程求出a,即可求椭圆M的方程;
代入方程求出a,即可求椭圆M的方程;(Ⅱ)先利用直线l的方向向量为
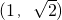 ,求出直线的斜率,设出直线方程;再与椭圆方程联立,求出B、C两点的坐标与m的关系;再求出B、C两点之间的线段长以及点A到BC的距离,代入△ABC面积的表达式,再结合不等式的有关知识求出△ABC面积的最大值即可.
,求出直线的斜率,设出直线方程;再与椭圆方程联立,求出B、C两点的坐标与m的关系;再求出B、C两点之间的线段长以及点A到BC的距离,代入△ABC面积的表达式,再结合不等式的有关知识求出△ABC面积的最大值即可.点评:本题主要考查直线与圆锥曲线的综合问题.第一问涉及到了求抛物线的焦点坐标,在求抛物线的焦点坐标时,一定注意先把抛物线方程转化为标准形式,再求解,避免出错.

练习册系列答案
相关题目
 的焦点是椭圆M的一个焦点,又点A
的焦点是椭圆M的一个焦点,又点A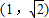 在椭圆M上.
在椭圆M上.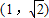 ,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.
,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.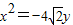 的焦点是椭圆M的一个焦点,又点A
的焦点是椭圆M的一个焦点,又点A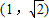 在椭圆M上.
在椭圆M上. ,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.
,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.