题目内容
已知椭圆M的对称轴为坐标轴,且(0,-
)是椭圆M的一个焦点,又点A(1,
)在椭圆M上.
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知直线l的斜率是
,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.
| 2 |
| 2 |
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知直线l的斜率是
| 2 |
分析:(Ⅰ)设出椭圆方程,代入A的坐标,即可求椭圆M的方程;
(Ⅱ)设出直线BC的方程,代入椭圆方程,利用韦达定理计算弦长,求出点A到BC的距离,可得三角形的面积,利用基本不等式,即可求得最值.
(Ⅱ)设出直线BC的方程,代入椭圆方程,利用韦达定理计算弦长,求出点A到BC的距离,可得三角形的面积,利用基本不等式,即可求得最值.
解答:解:(Ⅰ)由已知抛物线的焦点为(0,-
),故设椭圆方程为
+
=1.
将点A(1,
)代入方程得
+
=1,整理得a4-5a2+4=0,
解得a2=4或a2=1(舍).
故所求椭圆方程为
+
=1
(Ⅱ)设直线BC的方程为y=
x+m,设B(x1,y1),C(x2,y2)
代入椭圆方程并化简得4x2+2
mx+m2-4=0,
由△=8m2-16(m2-4)>0,可得m2<8①
由x1+x2=-
m,x1x2=
,
故|BC|=
|x1-x2|=
.
又点A到BC的距离为d=
,
故S△ABC=
|BC|d=
≤
•
=
,
当且仅当2m2=16-2m2,即m=±2时取等号(满足①式)
所以△ABC面积的最大值为
.
| 2 |
| y2 |
| a2 |
| x2 |
| a2-2 |
将点A(1,
| 2 |
| 2 |
| a2 |
| 1 |
| a2-2 |
解得a2=4或a2=1(舍).
故所求椭圆方程为
| y2 |
| 4 |
| x2 |
| 2 |
(Ⅱ)设直线BC的方程为y=
| 2 |
代入椭圆方程并化简得4x2+2
| 2 |
由△=8m2-16(m2-4)>0,可得m2<8①
由x1+x2=-
| ||
| 2 |
| m2-4 |
| 4 |
故|BC|=
| 3 |
| ||||
| 2 |
又点A到BC的距离为d=
| |m| | ||
|
故S△ABC=
| 1 |
| 2 |
| ||
| 4 |
| 1 | ||
4
|
| 2m2+(16-2m2) |
| 2 |
| 2 |
当且仅当2m2=16-2m2,即m=±2时取等号(满足①式)
所以△ABC面积的最大值为
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的焦点是椭圆M的一个焦点,又点A
的焦点是椭圆M的一个焦点,又点A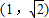 在椭圆M上.
在椭圆M上.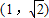 ,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.
,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.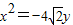 的焦点是椭圆M的一个焦点,又点A
的焦点是椭圆M的一个焦点,又点A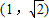 在椭圆M上.
在椭圆M上. ,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.
,若直线l与椭圆M交于B、C两点,求△ABC面积的最大值.