以下证明对于任意的.直线与的交点均在直线上——青夏教育精英家教网——

摘要：以下证明对于任意的.直线与的交点均在直线上

网址：http://m.1010jiajiao.com/timu_id_544267[举报]

已知双曲线C的中心在原点，D（1，0）是它的一个顶点，

)是它的一条渐近线的一个方向向量．
（1）求双曲线C的方程；
（2）若过点（-3，0）任意作一条直线与双曲线C交于A，B两点（A，B都不同于点D），求证：

为定值；
（3）对于双曲线Γ：

=1(a＞0，b＞0，a≠b)，E为它的右顶点，M，N为双曲线Γ上的两点（都不同于点E），且EM⊥EN，那么直线MN是否过定点？若是，请求出此定点的坐标；若不是，说明理由．然后在以下三个情形中选择一个，写出类似结论（不要求书写求解或证明过程）．
情形一：双曲线

=1(a＞0，b＞0，a≠b)及它的左顶点；
情形二：抛物线y²=2px（p＞0）及它的顶点；
情形三：椭圆

=1(a＞b＞0)及它的顶点．

查看习题详情和答案>>

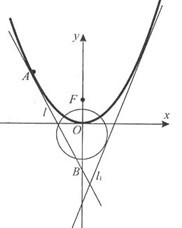（本题满分15分）如图，已知直线与抛物线和圆都相切，是的焦点.

（1）求与的值；

（2）设是上的一动点，以为切点作抛物线的切线，直线交轴于点，以为邻边作平行四边形，证明：点在一条定直线上；

（3）在（2）的条件下，记点所在的定直线为，直线与轴交点为，连接交抛物线于两点，求的面积的取值范围.

22。（本题满分15分）已知函数．

（1）求函数的图像在点处的切线方程；

（2）若，且对任意恒成立，求的最大值；

（3）当时，证明．

查看习题详情和答案>>

（2013•松江区二模）已知双曲线C的中心在原点，D（1，0）是它的一个顶点，

)是它的一条渐近线的一个方向向量．
（1）求双曲线C的方程；
（2）若过点（-3，0）任意作一条直线与双曲线C交于A，B两点（A，B都不同于点D），求证：

为定值；
（3）对于双曲线Γ：

=1(a＞0，b＞0，a≠b)，E为它的右顶点，M，N为双曲线Γ上的两点（都不同于点E），且EM⊥EN，那么直线MN是否过定点？若是，请求出此定点的坐标；若不是，说明理由．然后在以下三个情形中选择一个，写出类似结论（不要求书写求解或证明过程）．
情形一：双曲线

=1(a＞0，b＞0，a≠b)及它的左顶点；
情形二：抛物线y²=2px（p＞0）及它的顶点；
情形三：椭圆

=1(a＞b＞0)及它的顶点．

查看习题详情和答案>>

已知曲线C为顶点在原点，以x轴为对称轴，开口向右的抛物线，又点M（2，1）到抛物线C的准线的距离为，

（1）求抛物线C的方程；

（2）证明：过点M的任意一条直线与抛物线恒有公共点；

（3）若（2）中的直线（i=1，2，3， 4）分别与抛物线C交于上下两点，又点的纵坐标依次成公差不为0的等差数列，试分析的大小关系。

查看习题详情和答案>>

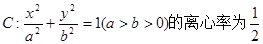已知椭圆，以原点为圆心，椭圆的短半轴为半径的圆与直线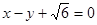相切.

（1）求椭圆C的方程；

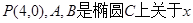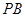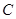（2）设轴对称的任意两个不同的点，连结交椭圆于另一点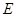，证明：直线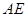与x轴相交于定点；

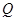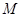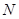（3）在（2）的条件下，过点的直线与椭圆交于、两点，求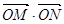的取值范围.

查看习题详情和答案>>