题目内容
已知曲线C为顶点在原点,以x轴为对称轴,开口向右的抛物线,又点M(2,1)到抛物线C的准线的距离为![]() ,
,
(1)求抛物线C的方程;
(2)证明:过点M的任意一条直线![]() 与抛物线恒有公共点;
与抛物线恒有公共点;
(3)若(2)中的直线![]() (i=1,2,3, 4)分别与抛物线C交于上下两点
(i=1,2,3, 4)分别与抛物线C交于上下两点![]() ,又点
,又点![]() 的纵坐标依次成公差不为0的等差数列,试分析
的纵坐标依次成公差不为0的等差数列,试分析![]() 的大小关系。
的大小关系。
解:(1)依题设抛物线C的方程为:![]()
由条件可知![]() 曲线C的方程为
曲线C的方程为![]()
(2)由题设,过M的li的方程为x-2+t(y-1)=0,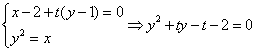
△=t2+4t+8>0,对于一切t成立,∴过点M的任意一条直线li与C恒有公共点。
(3)设![]() ,由定比分点坐标公式得:
,由定比分点坐标公式得: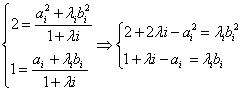 ,消去bi得
,消去bi得
| |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
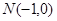 的直线
的直线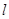 交曲线
交曲线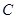 于
于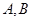 两点,又
两点,又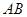 的中垂线交
的中垂线交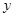 轴于点
轴于点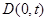 ,
,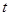 的取值范围。
的取值范围。