摘要：又椭圆的焦点在x轴上, ∴椭圆的标准方程为 -------------------------5分(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0), ------------------------6分
网址：http://m.1010jiajiao.com/timu_id_543426[举报]
已知在椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
（Ⅰ）求证：当a取定值时，点H必为定点；
（Ⅱ）如图所示，当点P在第二象限，以OP为直径的圆与直线AB相切，且四边形ABPH的面积等于3+
| 2 |
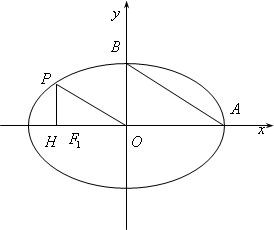
已知在椭圆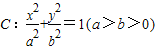
中，F1（-c，0）（c＞0）是椭圆的左焦点，A（a，0），B（0，b）分别是椭圆的右顶点和上顶点，点O是椭圆的中心．又点P在椭圆上，且满足条件：OP∥AB，点H是点P在x轴上的投影．
（Ⅰ）求证：当a取定值时，点H必为定点；
（Ⅱ）如图所示，当点P在第二象限，以OP为直径的圆与直线AB相切，且四边形ABPH的面积等于
，求椭圆的标准方程．
查看习题详情和答案>>
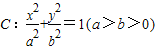中，F1（-c，0）（c＞0）是椭圆的左焦点，A（a，0），B（0，b）分别是椭圆的右顶点和上顶点，点O是椭圆的中心．又点P在椭圆上，且满足条件：OP∥AB，点H是点P在x轴上的投影．（Ⅰ）求证：当a取定值时，点H必为定点；
（Ⅱ）如图所示，当点P在第二象限，以OP为直径的圆与直线AB相切，且四边形ABPH的面积等于
，求椭圆的标准方程．
查看习题详情和答案>>
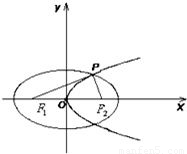
如图，设抛物线C1：y2=4mx（m＞0）的准线与x轴交于F1，焦点为F2；以F1，F2为焦点，离心率e=| 1 | 2 |
（1）当m=1时，求椭圆C2的方程；
（2）当△PF1F2的边长恰好是三个连续的自然数时，求抛物线方程；此时设⊙C1、⊙C2…⊙Cn是圆心在y2=4mx（m＞0）上的一系列圆，它们的圆心纵坐标分别为a1，a2…an，已知a1=6，a1＞a2＞…＞an＞0，又⊙Ck（k=1，2，…，n）都与y轴相切，且顺次逐个相邻外切，求数列{an}的通项公式． 查看习题详情和答案>>
的准线与x轴交于F1，焦点为F2；以F1，F2为焦点，离心率
的椭圆C2与抛物线C1在x轴上方的交点为P。 
当△PF1F2的边长恰好是三个连续的自然数时，求抛物线方程；此时设⊙C1、⊙C2……⊙Cn是圆心在
的椭圆C2与抛物线C1在x轴上方的交点为P．