Question

已知在椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)中，F₁（-c，0）（c＞0）是椭圆的左焦点，A（a，0），B（0，b）分别是椭圆的右顶点和上顶点，点O是椭圆的中心．又点P在椭圆上，且满足条件：OP∥AB，点H是点P在x轴上的投影．
（Ⅰ）求证：当a取定值时，点H必为定点；
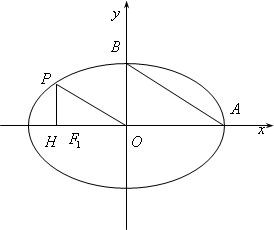
（Ⅱ）如图所示，当点P在第二象限，以OP为直径的圆与直线AB相切，且四边形ABPH的面积等于3+

2

，求椭圆的标准方程．

Answer 1

分析：（I）由kAB=-

b

a

，OP∥AB，得lOP：y=-

b

a

x，代入椭圆方程

x2

a2

+

y2

b2

=1，得x2=

a2

2

，由此能够证明为定值，点H必为定点．
（II）当点P在第二象限，点O到直线AB的距离等于

1

2

|OP|，由条件设直线AB的方程为：

x

a

+

y

b

=1，则点O到直线AB的距离为d=

ab

a2+b2

，由P(-

2

2

a，

2

2

b)，知|OP|=

2a2+2b2

2

，从而

ab

a2+b2

=

2a2+2b2

4

，由四边形ABPH的面积等于3+

2

，知S_ABPH=S_△ABO+S_OBPH=

1

2

ab+

1

2

×(

2

2

b+b)×

2

2

a=

3+ 2

4

ab=3+

2

．由此能够求出椭圆的标准方程．

解答：解：（I）由kAB=-

b

a

，OP∥AB，得lOP：y=-

b

a

x，代入椭圆方程

x2

a2

+

y2

b2

=1，得x2=

a2

2

，即x=±

2

2

a，
由y=-

b

a

x，得P点的坐标为(-

2

2

a，

2

2

b)或(

2

2

a，-

2

2

b)，（3分）
∵PH⊥x轴，∴H(-

2

2

a，0)或H(

2

2

a，0)，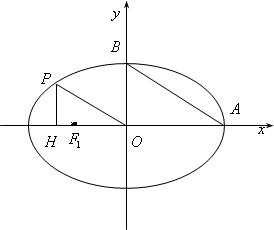
∵a为定值，∴点H必为定点．（6分）

（II）当点P在第二象限，以OP为直径的圆与直线AB相切，
即等价于点O到直线AB的距离等于

1

2

|OP|，（8分）
由条件设直线AB的方程为：

x

a

+

y

b

=1，
则点O到直线AB的距离为d=

ab

a2+b2

，
又由（I）可知P(-

2

2

a，

2

2

b)，所以|OP|=

2a2+2b2

2

，
从而

ab

a2+b2

=

2a2+2b2

4

，即a2+b2=2

2

ab①（10分）
又四边形ABPH的面积等于3+

2

，
则S_ABPH=S_△ABO+S_OBPH
=

1

2

ab+

1

2

×(

2

2

b+b)×

2

2

a=

3+ 2

4

ab=3+

2

整理得ab②（12分）
由①②解得a2=4(

2

+1)，b2=4(

2

-1)
所以所求椭圆的标准方程为

x2

4( 2 +1)

+

y2

4( 2 -1)

=1．（14分）

点评：本题考查圆与圆锥曲线的综合运用，解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．