网址:http://m.1010jiajiao.com/timu_id_538298[举报]
一、 BCCC,ADBA
二、 30 2 1
1  50 96 96
50 96 96 
三、 解答题
16 (1) 


ω

(2)


17 (I)以D为原点,DA,DC,DD1所在直线为x轴,y轴,z轴,建立系
E点坐标为(1,1,1).
(2) 略
(3)二面角D1―BF―C的余弦值为
18
(1) 
(2)

(3)(Ⅰ)
当且仅当 时,即x=7时等号成立.
时,即x=7时等号成立.
 到第7年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分
到第7年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分
(Ⅱ)
故到第10年,盈利额达到最大值,工厂获利102+12=114万元 ……11分
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.…12分
19(1)椭圆 的方程是:
的方程是: .
.
(2) ,
, ,
,
 为常数.
为常数.
20 (1)用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
至少有1人面试合格的概率是
(2)∴ 的分布列是
的分布列是

0
1
2
3





 的期望
的期望
21(1) (2)(2)①
(2)(2)①

 ,
, .
. 当
当 时,
时, . 假设
. 假设 ,则
,则 .
.
由数学归纳法证明 为常数数列,是等差数列,其通项为
为常数数列,是等差数列,其通项为 . ……8分
. ……8分
② ,
,  .
.
 当
当 时,
时, . 假设
. 假设 ,则
,则
 .
.
由数学归纳法,得出数列
 .……………10分
.……………10分
又 ,
, ,
,
即 ………12分
………12分



 .
.
 ,
, . ………………14分
. ………………14分
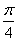 个单位,沿y轴向下平移
个单位,沿y轴向下平移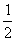 个单位,得到g(x)的图象,已知g(x)的图象关于
个单位,得到g(x)的图象,已知g(x)的图象关于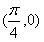 对称。
对称。(1)求ω的值;
(2)求g(x)在[0,4π]上的单调递增区间。
(本小题满分12分)向量a=(sinωx+cosωx,1),b=(f(x),simωx),其中0<ω<l,且a∥b.将f(x)的图象沿x轴向左平移![]() 个单位,沿y轴向下平移
个单位,沿y轴向下平移![]() 个单位,得到g(x)的图象,已知g(x)的图象关于(
个单位,得到g(x)的图象,已知g(x)的图象关于(![]() ,0)对称 (I)求ω的值; (Ⅱ)求g(x)在[0,4π]上的单调递增区间.
,0)对称 (I)求ω的值; (Ⅱ)求g(x)在[0,4π]上的单调递增区间.
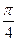 个单位,沿y轴向下平移
个单位,沿y轴向下平移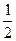 个单位,得到g(x)的图象,已知g(x)的图象关于(
个单位,得到g(x)的图象,已知g(x)的图象关于(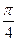 ,0)对称 (I)求ω的值; (Ⅱ)求g(x)在[0,4π]上的单调递增区间.
,0)对称 (I)求ω的值; (Ⅱ)求g(x)在[0,4π]上的单调递增区间.