摘要:一般地.三次函数的“拐点 是.它就是的对称中心.----------------------10分(或者:任何一个三次函数都有拐点,任何一个三次函数都有对称中心,任何一个三次函数平移后可以是奇函数---)都可以给分
网址:http://m.1010jiajiao.com/timu_id_538268[举报]
下列命题正确的个数是( )
①二次函数的极值点是唯一的,所以二次函数的极值点即最值点 ②f(x)=![]() 在(-∞,+∞)内是单调函数,所以f(x)在任何区间上都有最值 ③在区间[a,b]上,函数f(x)的极小值就是最小值 ④在闭区间[a,b]上,连续函数f(x)必有最大值与最小值
在(-∞,+∞)内是单调函数,所以f(x)在任何区间上都有最值 ③在区间[a,b]上,函数f(x)的极小值就是最小值 ④在闭区间[a,b]上,连续函数f(x)必有最大值与最小值
A.0 B.1 C.2 D.3
查看习题详情和答案>>对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f″(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有的同学发现“任何三次函数都有‘拐点’;任何三次函数都有对称中心;且对称中心就是‘拐点’”.请你根据这一发现判断下列命题:
(1)任意三次函数都关于点(-
,f(-
))对称;
(2)存在三次函数,f'(x)=0有实数解x0,(x0,f(x0))点为函数y=f(x)的对称中心;
(3)存在三次函数有两个及两个以上的对称中心;
(4)若函数g(x)=
x3-
x2-
,则g(
)+g(
)+g(
)+…+g(
)=-1006
其中正确命题的序号为( )
(1)任意三次函数都关于点(-
| b |
| 3a |
| b |
| 3a |
(2)存在三次函数,f'(x)=0有实数解x0,(x0,f(x0))点为函数y=f(x)的对称中心;
(3)存在三次函数有两个及两个以上的对称中心;
(4)若函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2013 |
| 2 |
| 2013 |
| 3 |
| 2013 |
| 2012 |
| 2013 |
其中正确命题的序号为( )
查看习题详情和答案>>
(2009•东营一模)对于三次函数f(x)=ax3+bx2+cx+d(a≠0).
定义:(1)设f''(x)是函数y=f(x)的导数y=f'(x)的导数,若方程f''(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”;
定义:(2)设x0为常数,若定义在R上的函数y=f(x)对于定义域内的一切实数x,都有f(x0+x)+f(x0-x)=2f(x0)成立,则函数y=f(x)的图象关于点(x0,f(x0))对称.
已知f(x)=x3-3x2+2x+2,请回答下列问题:
(1)求函数f(x)的“拐点”A的坐标
(2)检验函数f(x)的图象是否关于“拐点”A对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数G(x),使得它的“拐点”是(-1,3)(不要过程)
查看习题详情和答案>>
定义:(1)设f''(x)是函数y=f(x)的导数y=f'(x)的导数,若方程f''(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”;
定义:(2)设x0为常数,若定义在R上的函数y=f(x)对于定义域内的一切实数x,都有f(x0+x)+f(x0-x)=2f(x0)成立,则函数y=f(x)的图象关于点(x0,f(x0))对称.
已知f(x)=x3-3x2+2x+2,请回答下列问题:
(1)求函数f(x)的“拐点”A的坐标
(2)检验函数f(x)的图象是否关于“拐点”A对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数G(x),使得它的“拐点”是(-1,3)(不要过程)
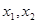 分别为三次函数
分别为三次函数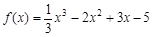 的极大值点和极小值点,则以
的极大值点和极小值点,则以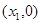 为顶点,
为顶点,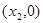 为焦点的双曲线的离心率
为焦点的双曲线的离心率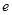 等于
等于
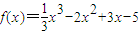 的极大值点和极小值点,则以(x1,0)为顶点,(x2,0)为焦点的双曲线的离心率e 等于 .
的极大值点和极小值点,则以(x1,0)为顶点,(x2,0)为焦点的双曲线的离心率e 等于 .