题目内容
若x1,x2分别为三次函数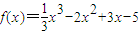 的极大值点和极小值点,则以(x1,0)为顶点,(x2,0)为焦点的双曲线的离心率e 等于 .
的极大值点和极小值点,则以(x1,0)为顶点,(x2,0)为焦点的双曲线的离心率e 等于 .
【答案】分析:求导数,确定函数的极值点,从而可得双曲线的顶点与焦点,进而可得双曲线的离心率.
解答:解:求导函数可得f′(x)=x2-4x2+3
令f′(x)=x2-4x2+3>0,可得x<1或x>3;令f′(x)=x2-4x2+3<0,可得1<x<3
∴1,3是函数的极值点
∴(1,0)为双曲线的顶点,(3,0)为双曲线的焦点
∴a=1,c=3
∴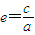 =3
=3
故答案为3.
点评:本题考查导数知识的运用,考查双曲线的几何性质,考查学生的计算的能力,属于中档题.
解答:解:求导函数可得f′(x)=x2-4x2+3
令f′(x)=x2-4x2+3>0,可得x<1或x>3;令f′(x)=x2-4x2+3<0,可得1<x<3
∴1,3是函数的极值点
∴(1,0)为双曲线的顶点,(3,0)为双曲线的焦点
∴a=1,c=3
∴
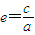 =3
=3故答案为3.
点评:本题考查导数知识的运用,考查双曲线的几何性质,考查学生的计算的能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 .
. ,③
,③