网址:http://m.1010jiajiao.com/timu_id_534866[举报]
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当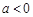 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
查看习题详情和答案>>
已知函数 .(
.( )
)
(1)若 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方,求
下方,求 的取值范围.
的取值范围.
【解析】第一问中,首先利用 在区间
在区间 上单调递增,则
上单调递增,则 在区间
在区间 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在区间
在区间 上单调递增,
上单调递增,
则 在区间
在区间 上恒成立. …………3分
上恒成立. …………3分
即 ,而当
,而当 时,
时, ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令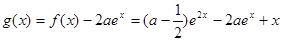 ,定义域为
,定义域为 .
.
在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得极值点
,得极值点 ,
, ,
,
当 ,即
,即 时,在(
时,在( ,+∞)上有
,+∞)上有 ,此时
,此时 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有 ,不合题意;
,不合题意;
当 ,即
,即 时,同理可知,
时,同理可知, 在区间
在区间 上递增,
上递增,
有 ,也不合题意;
…………11分
,也不合题意;
…………11分
② 若 ,则有
,则有 ,此时在区间
,此时在区间 上恒有
上恒有 ,从而
,从而 在区间
在区间 上是减函数;
上是减函数;
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得 的范围是
的范围是 . …………13分
. …………13分
综合①②可知,当 时,函数
时,函数 的图象恒在直线
的图象恒在直线 下方.
下方.
查看习题详情和答案>>
已知中心在坐标原点,焦点在 轴上的椭圆C;其长轴长等于4,离心率为
轴上的椭圆C;其长轴长等于4,离心率为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点 (0,1), 问是否存在直线
(0,1), 问是否存在直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ?若存在,求出
?若存在,求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【解析】本试题主要考查了椭圆的方程的求解,直线与椭圆的位置关系的运用。
第一问中,可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
第二问中,
假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得
代入1,2式中得到范围。
(Ⅰ) 可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
(Ⅱ) 假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得 ……② ……………………9分
……② ……………………9分
则 .
.
代入①式得,解得 ………………………………………12分
………………………………………12分
代入②式得 ,得
,得 .
.
综上(i)(ii)可知,存在这样的直线 ,其斜率k的取值范围是
,其斜率k的取值范围是
查看习题详情和答案>>