题目内容
(本题满分18分)第(1)小题满分4分,第(2)小题满分8分,第(3)小题满分6分。
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆![]() 。
。
若椭圆![]() ,判断
,判断![]() 与
与![]() 是否相似?如果相似,求出
是否相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
 写出与椭圆
写出与椭圆![]() 相似且短半轴长为
相似且短半轴长为![]() 的椭圆
的椭圆![]() 的方程;若在椭圆
的方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围?
的取值范围?
如图:直线![]() 与两个“相似椭圆”
与两个“相似椭圆”![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,证明:
,证明:![]()
解:(1)椭圆![]() 与
与![]() 相似。-------------------2分
相似。-------------------2分
因为椭圆![]() 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为![]() 的等腰三角形,而椭圆
的等腰三角形,而椭圆![]() 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为![]() 的等腰三角形,因此两个等腰三角形相似,且相似比为
的等腰三角形,因此两个等腰三角形相似,且相似比为![]() -------------------4分
-------------------4分
(2)椭圆![]() 的方程为:
的方程为:![]() -------------------6分
-------------------6分
设![]() ,点
,点![]() ,
,![]() 中点为
中点为![]() ,
,
则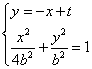 ,所以
,所以![]() -------------------8分
-------------------8分
则![]() -------------------9分
-------------------9分
因为中点在直线![]() 上,所以有
上,所以有![]() ,
,![]() -------------------10分
-------------------10分
即直线![]() 的方程为:
的方程为:![]() ,
,
由题意可知,直线![]() 与椭圆
与椭圆![]() 有两个不同的交点,
有两个不同的交点,
即方程![]() 有两个不同的实数解,
有两个不同的实数解,
所以![]() ,即
,即![]() -------------------12分
-------------------12分
(3)证明:
①直线![]() 与
与![]() 轴垂直时,易得线段AB与CD的中点重合,所以
轴垂直时,易得线段AB与CD的中点重合,所以![]() ;-------------------14分
;-------------------14分
②直线![]() 不与
不与![]() 轴垂直时,设直线
轴垂直时,设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,
线段AB的中点![]() ,
,
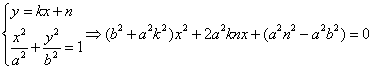 -------------------15分
-------------------15分

![]() 线段AB的中点为
线段AB的中点为![]() -------------------16分
-------------------16分
同理可得线段CD的中点为![]() ,-------------------17分
,-------------------17分
即线段AB与CD的中点重合,所以![]() -------------------18分
-------------------18分


 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当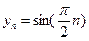 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
( 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
. ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
( ,
,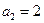 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
(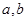 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
.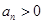 ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
(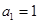 ,
,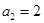 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列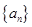 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”. ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”; 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求