网址:http://m.1010jiajiao.com/timu_id_533692[举报]
 (2008?天津)(1)用螺旋测微器测金属导线的直径,其示数如图所示,该金属导线的直径为
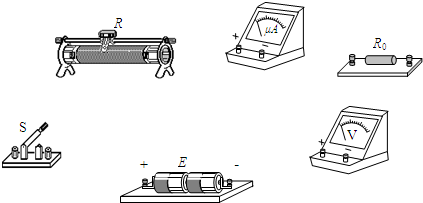
(2008?天津)(1)用螺旋测微器测金属导线的直径,其示数如图所示,该金属导线的直径为(2)用下列器材组装成描绘电阻R0伏安特性曲线的电路,请将实物图连线成为实验电路.
微安表μA(量程200μA,内阻约200Ω);
电压表V(量程3V,内阻约10kΩ);
电阻R0(阻值约20kΩ);
滑动变阻器R(最大阻值50Ω,额定电流1A);
电源E(电动势3V,内阻不计);
开关S及导线若干.
(3)某同学用单摆测重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两点,坐标如图所示.他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=
| 4π2(LB-LA) | ||||
|
| 4π2(LB-LA) | ||||
|
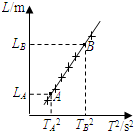
为了测定气垫导轨上滑块的加速度,滑块上安装了宽度为3.0 cm的遮光板,如图1-1-4所示,滑块在牵引力作用下先后匀加速通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为Δt1=0.30 s,通过第二个光电门的时间为Δt2=0.10 s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为Δt=3.0 s。试估算:

图1-1-4
(1)滑块的加速度多大?
(2)两个光电门之间的距离是多少?
解析:(1)遮光板通过第一个光电门的速度
v1=![]() =
=![]() m/s=0.10 m/s
m/s=0.10 m/s
遮光板通过第二个光电门的速度
v2=![]() =
=![]() m/s=0.30 m/s
m/s=0.30 m/s
故滑块的加速度a=![]() ≈0.067 m/s2。
≈0.067 m/s2。
(2)两个光电门之间的距离x=![]() Δt=0.6 m。
Δt=0.6 m。
答案:(1)0.067 m/s2 (2)0.6 m
查看习题详情和答案>>解析 (1)设木板第一次上升过程中,物块的加速度为a物块,由牛顿第二定律kmgsin θ-mgsin θ=ma物块
解得a物块=(k-1)gsin θ,方向沿斜面向上
(2)设以地面为零势能面,木板第一次与挡板碰撞时的速度大小为v1
由机械能守恒得:![]() ×2mv
×2mv![]() =2mgH
=2mgH
解得v1=![]()
设木板弹起后的加速度为a板,由牛顿第二定律得:
a板=-(k+1)gsin θ
木板第一次弹起的最大路程s1=![]() =
=![]()
木板运动的路程s=![]() +2s1=
+2s1=![]()
(3)设物块相对木板滑动距离为L
根据能量守恒mgH+mg(H+Lsin θ)=kmgLsin θ
摩擦力对木板及物块做的总功W=-kmgLsin θ
解得W=-![]()
答案 (1)(k-1)gsin θ;方向沿斜面向上
(2)![]() (3)-
(3)-![]()
解析 (1)整个装置沿斜面向上做匀速运动时,即整个系统处于平衡状态,
则研究A物体:f=mAgsin θ=2 N,
研究整体:F=(mA+mB)gsin θ+μ2(mA+mB)gcos θ=21 N.
(2)整个装置沿斜面向上做匀加速运动,且A、B恰好没有相对滑动,则说明此时A、B之间恰好达到最大静摩擦力,
研究A物体:
fmax=f滑=μ1mAgcos θ=2.4 N,
fmax-mAgsin θ=mAa,
解得a=1 m/s2,
研究整体:F-(mA+mB)gsin θ-μ2(mA+mB)gcos θ=(mA+mB)a,
解得F=23.4 N.
答案 (1)2 N 21 N (2)2.4 N 23.4 N
查看习题详情和答案>>