题目内容
解析 (1)设木板第一次上升过程中,物块的加速度为a物块,由牛顿第二定律kmgsin θ-mgsin θ=ma物块
解得a物块=(k-1)gsin θ,方向沿斜面向上
(2)设以地面为零势能面,木板第一次与挡板碰撞时的速度大小为v1
由机械能守恒得:![]() ×2mv
×2mv![]() =2mgH
=2mgH
解得v1=![]()
设木板弹起后的加速度为a板,由牛顿第二定律得:
a板=-(k+1)gsin θ
木板第一次弹起的最大路程s1=![]() =
=![]()
木板运动的路程s=![]() +2s1=
+2s1=![]()
(3)设物块相对木板滑动距离为L
根据能量守恒mgH+mg(H+Lsin θ)=kmgLsin θ
摩擦力对木板及物块做的总功W=-kmgLsin θ
解得W=-![]()
答案 (1)(k-1)gsin θ;方向沿斜面向上
(2)![]() (3)-
(3)-![]()
(2013·福建三明模拟)光滑曲面轨道置于高度为H=1.8 m的平台上,其末端切线水平;另有一长木板两端分别搁在轨道末端点和水平地面间,构成倾角为θ=37°的斜面,如图4-3-21所示.一个可视作质点的质量为m=1 kg的小球,从光滑曲面上由静止开始下滑(不计空气阻力,g取10 m/s2,sin 37°≈0.6,cos 37°≈0.8)
(1)若小球从高h=0.2 m处下滑,则小球离开平台时速度v0的大小是多少?
(2)若小球下滑后正好落在木板的末端,则释放小球的高度h为多大?
(3)试推导小球下滑后第一次撞击木板时的动能与它下滑高度h的关系表达式,并在图4-3-22 中作出Ek-h图象.
 图4-3-21
图4-3-21
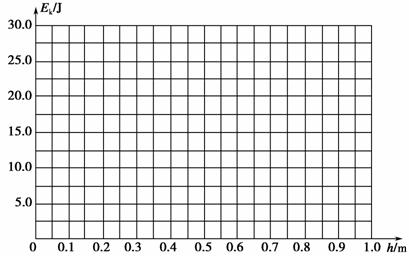
图4-3-22

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
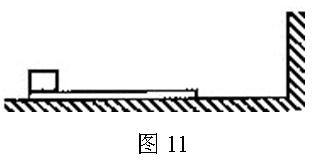
 倍,重物与木板间的动摩擦因数为
倍,重物与木板间的动摩擦因数为 。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求
。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求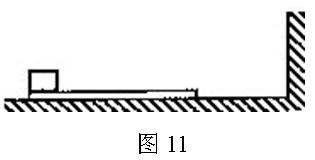
 。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求
。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求