网址:http://m.1010jiajiao.com/timu_id_53325[举报]
①对于任意正实数a,b,∵(
| a |
| b |
| ab |
| ab |
只有当a=b时,等号成立.
②结论:在a+b≥2
| ab |
| p |
只有当a=b时,a+b有最小值2
| p |
(Ⅱ)结论运用:根据上述内容,回答下列问题:(提示:在答题卡上作答)
①若m>0,只有当m=
| 1 |
| m |
②若m>1,只有当m=
| 8 |
| m-1 |
(Ⅲ)探索应用:
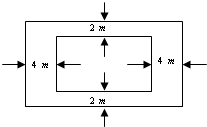
学校要建一个面积为392m2的长方形游泳池,并且在四周要修建出宽为2m和4m的小路(如图).问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值.
(1)阅读理解:①对于任意正实数 ,
, 只有当
只有当 时,等号成立.
时,等号成立.
②结论:在 (
( 均为正实数)中,若
均为正实数)中,若 为定值
为定值 , 则
, 则 ,只有当
,只有当 时,
时, 有最小值
有最小值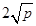 .
.
(2)结论运用:根据上述内容,回答下列问题:(提示:在答题卡上作答)
①若 ,只有当
,只有当 __________时,
__________时, 有最小值__________.
有最小值__________.
②若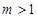 ,只有当
,只有当 __________时,
__________时, 有最小值__________.
有最小值__________.
(3)探索应用:学校要建一个面积为392 的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值。
的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值。
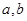 ,
, 只有当
只有当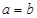 时,等号成立.
时,等号成立.
②结论:在
 (
(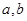 均为正实数)中,若
均为正实数)中,若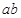 为定值
为定值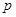 , 则
, 则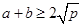 ,只有当
,只有当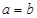 时,
时, 有最小值
有最小值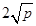 .
.(2)结论运用:根据上述内容,回答下列问题:(提示:在答题卡上作答)
①若
 ,只有当
,只有当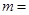 __________时,
__________时,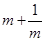 有最小值__________.
有最小值__________.②若
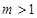 ,只有当
,只有当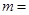 __________时,
__________时,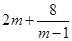 有最小值__________.
有最小值__________.(3)探索应用:学校要建一个面积为392
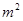 的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值。
的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值。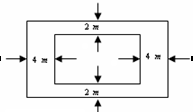
已知数列 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d, 为其前n项和,且满足
为其前n项和,且满足 ,
, .数列
.数列 满足
满足 ,
, ,
, 为数列
为数列 的前n项和.
的前n项和.
(1)求数列 的通项公式
的通项公式 和数列
和数列 的前n项和
的前n项和 ;
;
(2)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在正整数
 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问利用在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 时,
时, 满足
满足 ,
,
 ,
,

第二问,①当n为偶数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等号在n=2时取得.
,等号在n=2时取得.
 此时
此时 需满足
需满足 .
.
②当n为奇数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是随n的增大而增大, n=1时
是随n的增大而增大, n=1时 取得最小值-6.
取得最小值-6.
 此时
此时 需满足
需满足 .
.
第三问 ,
,
若 成等比数列,则
成等比数列,则 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
(1)(法一)在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 时,
时, 满足
满足 ,
,
 ,
,
 .
.
(2)①当n为偶数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等号在n=2时取得.
,等号在n=2时取得.
 此时
此时 需满足
需满足 .
.
②当n为奇数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是随n的增大而增大, n=1时
是随n的增大而增大, n=1时 取得最小值-6.
取得最小值-6.
 此时
此时 需满足
需满足 .
.
综合①、②可得 的取值范围是
的取值范围是 .
.
(3) ,
,
若 成等比数列,则
成等比数列,则 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
又 ,且m>1,所以m=2,此时n=12.
,且m>1,所以m=2,此时n=12.
因此,当且仅当m=2,
n=12时,数列 中的
中的 成等比数列
成等比数列
查看习题详情和答案>>