摘要:解:(Ⅰ) -----------------------3分
网址:http://m.1010jiajiao.com/timu_id_53309[举报]
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
(Ⅰ)设{an}是集合![]() 中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
将数列{an}各项按照上小下大,左小右大的原则写成如下的三角形数表:
(i)写出这个三角形数表的第四行、第五行各数;
(ii)求a100.
(Ⅱ)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
设{bn}是集合![]() 中所有的数从小到大排列成的数列,已知bk =1160,求k.
中所有的数从小到大排列成的数列,已知bk =1160,求k.
(1)分解因式:x2-2xy+y2+2x-2y-3.
(2)求sin30°-tan0°+ctg
-cos2
的值,
(3)求函数y=
的定义域.
(4)已知直圆锥体的底面半径等于1cm,母线的长等于2cm,求它的体积.
(5)计算:10(2+
)-1-(
)-
+30(
)
(
)
的值.
查看习题详情和答案>>
(2)求sin30°-tan0°+ctg
| π |
| 4 |
| 5π |
| 6 |
(3)求函数y=
| lg(25-5x) |
| x+1 |
(4)已知直圆锥体的底面半径等于1cm,母线的长等于2cm,求它的体积.
(5)计算:10(2+
| 5 |
| 1 |
| 500 |
| 1 |
| 2 |
| 125 |
| 9 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
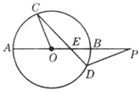 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)A(不等式选做题)如果关于x的不等式|x-3|-|x-4|<a的解集不是空集,则实数a的取值范围是
B(几何证明选做题)如图,圆O的割线PBA过圆心O,弦CD交AB于点E,且△COE~△PDE,PB=OA=2,则PE的长等于
C(极坐标系与参数方程选做题)圆ρ=2COSθ的圆心到直线
|

 (理)已知函数f(x)=
(理)已知函数f(x)=| ln(2-x2) |
| |x+2|-2 |
(1)试判断f(x)的奇偶性并给予证明;
(2)求证:f(x)在区间(0,1)单调递减;
(3)如图给出的是与函数f(x)相关的一个程序框图,试构造一个公差不为零的等差数列
{an},使得该程序能正常运行且输出的结果恰好为0.请说明你的理由.
(文)如图,在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
(1)求证:F<0;
(2)若四边形ABCD的面积为8,对角线AC的长为2,且
| AB |
| AD |
(3)设四边形ABCD的一条边CD的中点为G,OH⊥AB且垂足为H.试用平面解析几何的研究方法判
断点O、G、H是否共线,并说明理由. 查看习题详情和答案>>