摘要:解得.可知E为BC中点.
网址:http://m.1010jiajiao.com/timu_id_531466[举报]
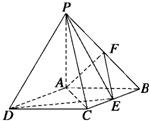 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=| 3 |
(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅱ)当E为BC中点时,求异面直线PC与DE所成角的余弦值;
(Ⅲ)求证:无论点E在边BC的何处,都有PE⊥AF. 查看习题详情和答案>>
 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD,PO⊥平面ABCD.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD,PO⊥平面ABCD.(1)求证:BD⊥PE;
(2)若AO=2PO,求二面角D-PE-B的余弦值.
 如图,长方体ABCD-A1B1C1D1中,AA1=
如图,长方体ABCD-A1B1C1D1中,AA1=| 2 |
(1)求证:平面A1DE⊥平面A1AE;
(2)求异面直线A1E、CD所成的角;
(3)设△A1DE的重心为G,问是否存在实数λ,使得
| AM |
| AD |
MG⊥平面A1ED同时成立?若存在,求出λ的值;若不存在,说明理由.
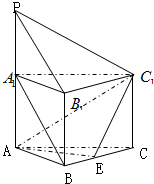 如图,正三棱柱ABC-A1B1C1的每条棱长均为2,PA1⊥平面ABC,PA1=2,E为BC中点.
如图,正三棱柱ABC-A1B1C1的每条棱长均为2,PA1⊥平面ABC,PA1=2,E为BC中点.(1)求证:PB1∥面AEC1;
(2)求PB1与C1E所成的角;
(3)求点A到面PB1C1的距离.
三棱锥D-ABC中,DA⊥平面ABC,DA=4,AB=AC=2,AB⊥AC,E为BC中点,F为CD中点,则异面直线AE与BF所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|