题目内容
 如图,长方体ABCD-A1B1C1D1中,AA1=
如图,长方体ABCD-A1B1C1D1中,AA1=| 2 |
(1)求证:平面A1DE⊥平面A1AE;
(2)求异面直线A1E、CD所成的角;
(3)设△A1DE的重心为G,问是否存在实数λ,使得
| AM |
| AD |
MG⊥平面A1ED同时成立?若存在,求出λ的值;若不存在,说明理由.
分析:(1)根据二面角的平面角的定义,可得二面角的棱垂直于平面角所在的平面,得线面垂直,再由线面垂直⇒面面垂直.
(2)建立空间直角坐标系,给出相关点与向量的坐标,根据AE⊥DE,求出m的值,再求向量夹角的余弦值.
(3)根据
=λ
,写出M的坐标,求出
的坐标,根据条件MG⊥DE,MG⊥EA1确定是否存在λ.
(2)建立空间直角坐标系,给出相关点与向量的坐标,根据AE⊥DE,求出m的值,再求向量夹角的余弦值.
(3)根据
| AM |
| AD |
| MG |
解答:解:(1)证明:∵∠AEA1为二面角A1-ED-A的平面角
∴A1E⊥ED,AE⊥ED,A1E∩AE=E,∴ED⊥平面A1AE,DE?平面A1DE,
∴平面A1DE⊥平面A1AE.
(2)如图建立空间直角坐标系,则A(0,0,0),A1(0,0,
),B(1,0,0),D(0,m,0),E(1,
,0).
=(1,
,-
),ED=(-1,
,0),AE=(1,
,0),
∵AE⊥ED,
•
=0,即-1+
=0⇒m=2,则C(1,2,0),
=(-1,0,0)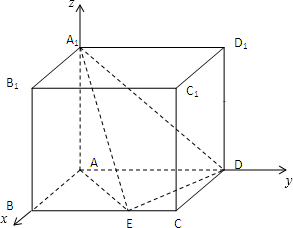
=(-1,-1,
),cos<
,
>=
=
=
,
∴异面直线A1E、CD所成的角为60°.
(3)依题意得:G(
,1,
),
=λ
,∴M(0,2λ,0).
=(
,1-2λ,
),
假设存在λ满足题设条件,则
•EA1=0,且
•
=0,
即
,
解得λ=
,
故存在实数λ=
,使得
=λ
,且MG⊥平面A1ED同时成立.
∴A1E⊥ED,AE⊥ED,A1E∩AE=E,∴ED⊥平面A1AE,DE?平面A1DE,
∴平面A1DE⊥平面A1AE.
(2)如图建立空间直角坐标系,则A(0,0,0),A1(0,0,
| 2 |
| m |
| 2 |
| A1E |
| m |
| 2 |
| 2 |
| m |
| 2 |
| m |
| 2 |
∵AE⊥ED,
| AE |
| ED |
| m2 |
| 4 |
| CD |

| EA1 |
| 2 |
| EA1 |
| CD |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
∴异面直线A1E、CD所成的角为60°.
(3)依题意得:G(
| 1 |
| 3 |
| ||
| 3 |
| AM |
| AD |
| MG |
| 1 |
| 3 |
| ||
| 3 |
假设存在λ满足题设条件,则
| MG |
| MG |
| ED |
即
|
解得λ=
| 1 |
| 3 |
故存在实数λ=
| 1 |
| 3 |
| AM |
| AD |
点评:本题考查了利用向量坐标运算求异面直线所成的角,考查用向量法解决立体几何中的存在性问题,考查了学生的运算能力及逻辑推理能力,本题对向量的工具作用体现较好.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点. 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )