题目内容
三棱锥D-ABC中,DA⊥平面ABC,DA=4,AB=AC=2,AB⊥AC,E为BC中点,F为CD中点,则异面直线AE与BF所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
分析:根据DA,AB,AC两两垂直,建立空间直角坐标系,写出相关点的坐标,求出
,
的坐标表示,利用向量坐标运算求解.
| AE |
| BF |
解答:解:建立空间直角坐标系如图:
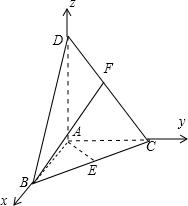
∵DA=4,AB=AC=2,AB⊥AC,E为BC中点,F为CD中点,
∴B(2,0,0),C(0,2,0),A(0,0,0),D(0,0,4),
E(1,1,0),F(0,1,2),
∴
=(1,1,0),
=(-2,1,2),
cos<
,
>=
=-
,
∴异面直线AE与BF所成角的余弦值为
.
故答案是
.

∵DA=4,AB=AC=2,AB⊥AC,E为BC中点,F为CD中点,
∴B(2,0,0),C(0,2,0),A(0,0,0),D(0,0,4),
E(1,1,0),F(0,1,2),
∴
| AE |
| BF |
cos<
| AE |
| BF |
| -2+1 | ||
|
| ||
| 6 |
∴异面直线AE与BF所成角的余弦值为
| ||
| 6 |
故答案是
| ||
| 6 |
点评:本题考查了异面直线所成角的求法,利用向量坐标运算求异面直线所成的角是常用方法,要熟练掌握.

练习册系列答案
相关题目
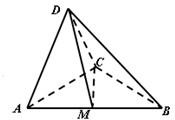 如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=
如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=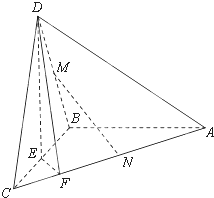 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC. 如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.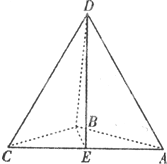 如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ.
如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ.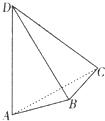 如图,在三棱锥D-ABC中,已知BC丄AD,BC=2,AD=6,AB+BD=AC+CD=10,则三棱锥D一ABC的体积的最大值是
如图,在三棱锥D-ABC中,已知BC丄AD,BC=2,AD=6,AB+BD=AC+CD=10,则三棱锥D一ABC的体积的最大值是