摘要：在Rt△EAH中.AE=.所以 当AH最短时.∠EHA最大.即 当AH⊥PD时.∠EHA最大.
网址：http://m.1010jiajiao.com/timu_id_531212[举报]
如图，在Rt△ABC中，∠ABC=90°，BA=BC=2，AE⊥平面ABC，CD⊥平面ABC，CE交AD于点P．（1）若AE=CD，点M为BC的中点，求证：直线MP∥平面EAB
（2）若AE=2，CD=1，求锐二面角E-BC-A的平面角的余弦值．
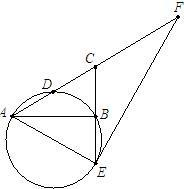已知：如图，在Rt△ABC中，∠ABC=90°，D是AC的中点，CB的延长线交过A、B、D三点的圆于点E．（1）判断线段AE与CE之间的数量关系，并加以证明；
（2）若过A、B、D三点的圆记为⊙O，过E点作⊙O的切线交AC的延长线于点F，且CD：CF=1：2，求：cosF的值． 查看习题详情和答案>>
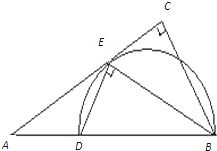
如图，在Rt△ABC中，∠ACB=90°，∠B=30°，D，E分）别为AB，CD的中点，AE的延长线交CB于F．现将△ACD沿CD折起，折成二面角A-CD-B，连接AF．（Ⅰ）求证：平面AEF⊥平面CBD；
（Ⅱ）当AC⊥BD时，求二面角A-CD-B大小的余弦值． 查看习题详情和答案>>
如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．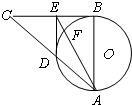
如图：在Rt∠ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作DE⊥BC，垂足为E，连接AE交⊙O于点F，求证：BE•CE=EF•EA．