摘要:求证:点Q落在双曲线=1上,
网址:http://m.1010jiajiao.com/timu_id_530616[举报]
设P(a,b)(b≠0)是平面直角坐标系xOy中的点,l是经过原点与点(1,b)的直线,记Q是直线l与抛物线x2=2py(p≠0)的异于原点的交点,
(1)若a=1,b=2,p=2,求点Q的坐标;
(2)若点P(a,b)(ab≠0)在椭圆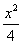 +y2=1上,p=
+y2=1上,p=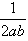 ,求证:点Q落在双曲线4x2-4y2=1上;
,求证:点Q落在双曲线4x2-4y2=1上;
(3)若动点P(a,b)满足ab≠0,p=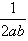 ,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。
,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。
查看习题详情和答案>>
(1)若a=1,b=2,p=2,求点Q的坐标;
(2)若点P(a,b)(ab≠0)在椭圆
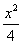 +y2=1上,p=
+y2=1上,p=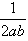 ,求证:点Q落在双曲线4x2-4y2=1上;
,求证:点Q落在双曲线4x2-4y2=1上;(3)若动点P(a,b)满足ab≠0,p=
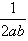 ,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。
,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。