网址:http://m.1010jiajiao.com/timu_id_530333[举报]
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求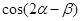 .
.
【解析】本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角关系是
,得到三角关系是 ,结合
,结合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,结合二倍角公式
,结合二倍角公式 ,和
,和 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴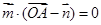 ,即
,即 ① …………2分
① …………2分
又 ② 由①②联立方程解得,
② 由①②联立方程解得,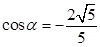 ,
,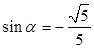 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即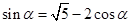 ,①……2分
,①……2分
又 ②
②
将①代入②中,可得 ③ …………………4分
③ …………………4分
将③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,从而
,从而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
综上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
综上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
查看习题详情和答案>>
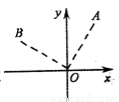
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点
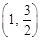 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存过点 (2,1)的直线
(2,1)的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【解析】第一问利用设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得
第二问若存在直线 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .解得。
.解得。
解:⑴设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得 ,故椭圆
,故椭圆 的方程为
的方程为 .……………………4分
.……………………4分
⑵若存在直线 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .
.
又 ,
,
因为 ,即
,即 ,
,
所以
 .
.
即 .
.
所以 ,解得
,解得 .
.
因为A,B为不同的两点,所以k=1/2.
于是存在直线L1满足条件,其方程为y=1/2x
查看习题详情和答案>>
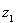
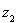
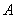

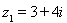
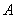


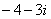
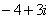
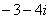
 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.  ,证明:
,证明: .
. ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。 .……4分
.……4分 ……8分
……8分 ,∴
,∴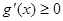 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分 ,即
,即