摘要:所以.=(0.y1+y2)=0.
网址:http://m.1010jiajiao.com/timu_id_530225[举报]
 如图所示,已知一次函数y=kx+b(b>0)与二次函数y=
如图所示,已知一次函数y=kx+b(b>0)与二次函数y=| 1 |
| 2 |
| AF |
| FB |
(1)求
| OA |
| OB |
(2)当t=
| 3 |
| 2 |
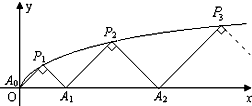 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
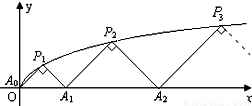
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线 上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△A0A1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A0为坐标原点).
上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△A0A1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A0为坐标原点).
(1)写出an-1、an和xn之间的等量关系,以及an-1、an和yn之间的等量关系;
(2)求证: (n∈N*);
(n∈N*);
(3)设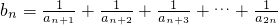 ,对所有n∈N*,bn<log8t恒成立,求实数t的取值范围.
,对所有n∈N*,bn<log8t恒成立,求实数t的取值范围.
查看习题详情和答案>>
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线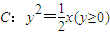 上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△AA1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A为坐标原点).
上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△AA1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A为坐标原点).
(1)写出an-1、an和xn之间的等量关系,以及an-1、an和yn之间的等量关系;
(2)求证: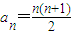 (n∈N*);
(n∈N*);
(3)设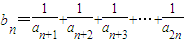 ,对所有n∈N*,bn<log8t恒成立,求实数t的取值范围.
,对所有n∈N*,bn<log8t恒成立,求实数t的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
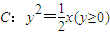 上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△AA1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A为坐标原点).
上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△AA1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A为坐标原点).(1)写出an-1、an和xn之间的等量关系,以及an-1、an和yn之间的等量关系;
(2)求证:
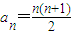 (n∈N*);
(n∈N*);(3)设
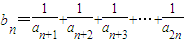 ,对所有n∈N*,bn<log8t恒成立,求实数t的取值范围.
,对所有n∈N*,bn<log8t恒成立,求实数t的取值范围. 查看习题详情和答案>>
查看习题详情和答案>>
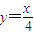 上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.
上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.