摘要:[解析]本小题主要考查直线与椭圆的位置关系.轨迹方程.不等式等基本知识.考查运算能力和综合解题能力.满分14分.解法一:(Ⅰ)由题设a=2,c=1,从而b2=a2-c2=3,
网址:http://m.1010jiajiao.com/timu_id_530144[举报]
已知△ 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(1)
若 , 求
, 求 的值;
的值;
(2)
若△ 的面积
的面积 求
求 的值.
的值.
【解析】本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识,考查运算求解能力。第一问中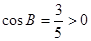 ,得到正弦值
,得到正弦值 ,再结合正弦定理可知,
,再结合正弦定理可知, ,得到
,得到 (2)中
(2)中 即
即 所以c=5,再利用余弦定理
所以c=5,再利用余弦定理 ,得到b的值。
,得到b的值。
解: (1)∵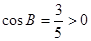 , 且
, 且 , ∴
, ∴  . 由正弦定理得
. 由正弦定理得 , ∴
, ∴ .
.
(2)∵ ∴
∴ . ∴c=5
. ∴c=5
由余弦定理得 ,
,
∴ 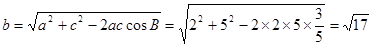
查看习题详情和答案>>
已知 是等差数列,其前n项和为
是等差数列,其前n项和为 ,
,  是等比数列,且
是等比数列,且


(I)求数列 与
与 的通项公式;
的通项公式;
(II)记 求证:
求证: ,
, 。
。
【考点定位】本小题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识.考查化归与转化的思想方法.考查运算能力、推理论证能力.
查看习题详情和答案>>
(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
查看习题详情和答案>>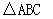 中,内角A,B,C所对的分别是a,b,c。已知a=2,c=
中,内角A,B,C所对的分别是a,b,c。已知a=2,c=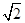 ,cosA=
,cosA= .
.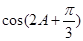 的值。
的值。