摘要:(Ⅱ)设直线y=kx+1与C交于A.B两点..k为何值时此时||的值是多少?[解析]本小题主要考查平面向量.椭圆的定义.标准方程及直线与椭圆位置关系等基础知识.考查综合运用解析几何知识解决问题的能力.
网址:http://m.1010jiajiao.com/timu_id_530068[举报]
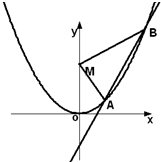 如图,已知直线L:y=kx-1与抛物线C:y=x2,相交于两点A、B,设点M(0,2),△MAB的面积为S.
如图,已知直线L:y=kx-1与抛物线C:y=x2,相交于两点A、B,设点M(0,2),△MAB的面积为S.(1)若直线L上与M连线距离为1的点至多存在一个,求S的范围.
(2)若直线L上与M连线的距离为1的点有两个,分别记为C、D,且满足S≥λ|CD|恒成立,求正数λ的范围.
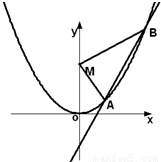
如图,已知直线L:y=kx-1与抛物线C:y=x2,相交于两点A、B,设点M(0,2),△MAB的面积为S.
(1)若直线L上与M连线距离为1的点至多存在一个,求S的范围.
(2)若直线L上与M连线的距离为1的点有两个,分别记为C、D,且满足S≥λ|CD|恒成立,求正数λ的范围.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)若直线L上与M连线距离为1的点至多存在一个,求S的范围.
(2)若直线L上与M连线的距离为1的点有两个,分别记为C、D,且满足S≥λ|CD|恒成立,求正数λ的范围.
 查看习题详情和答案>>
查看习题详情和答案>>
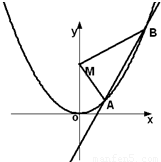
如图,已知直线L:y=kx-1与抛物线C:y=x2,相交于两点A、B,设点M(0,2),△MAB的面积为S.
(1)若直线L上与M连线距离为1的点至多存在一个,求S的范围.
(2)若直线L上与M连线的距离为1的点有两个,分别记为C、D,且满足S≥λ|CD|恒成立,求正数λ的范围.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)若直线L上与M连线距离为1的点至多存在一个,求S的范围.
(2)若直线L上与M连线的距离为1的点有两个,分别记为C、D,且满足S≥λ|CD|恒成立,求正数λ的范围.
 查看习题详情和答案>>
查看习题详情和答案>>