题目内容
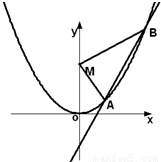
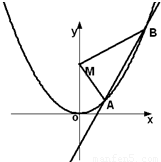
如图，已知直线L：y=kx-1与抛物线C：y=x2，相交于两点A、B，设点M（0，2），△MAB的面积为S．（1）若直线L上与M连线距离为1的点至多存在一个，求S的范围．
（2）若直线L上与M连线的距离为1的点有两个，分别记为C、D，且满足S≥λ|CD|恒成立，求正数λ的范围．
【答案】分析：（1）利用直线L与抛物线相交，直线L上与M连线距离为1的点至多存在一个，确定k的范围，表示出S，即可求S的范围．
（2）条件等价于λ≤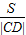
，求出相应函数的最小值，即可求正数λ的范围．
解答：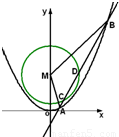
解：（1）由已知，直线L与抛物线相交，由
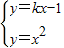可得x2-kx+1=0，∴△=k2-4＞0，即k2＞4…（1）
又直线L与以M为圆心的单位圆相离或相切，所以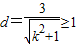
，即k2≤8…（2）
由（1）（2）得：4＜k2≤8
∵
=
=
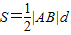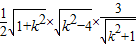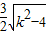
∴S∈（0，3]；…（7分）
（2）由题意可知，当直线L与以M为圆心的单位圆相交于点C，D时，可得k2＞8，且|CD|=2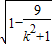
=2
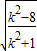
令f（k）=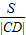
=
，
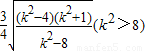令t=k2-8（t＞0），则y=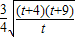
=
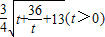，当且仅当k=
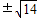取到最小值是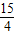
所以，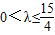
…（14分）
点评：本题考查直线与圆的位置关系，考查三角形面积的计算，考查基本不等式的运用，考查学生分析解决问题的能力，属于中档题．
（2）条件等价于λ≤
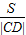，求出相应函数的最小值，即可求正数λ的范围．解答：
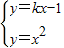解：（1）由已知，直线L与抛物线相交，由可得x2-kx+1=0，∴△=k2-4＞0，即k2＞4…（1）又直线L与以M为圆心的单位圆相离或相切，所以
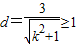，即k2≤8…（2）由（1）（2）得：4＜k2≤8
∵
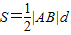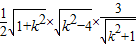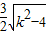
==∴S∈（0，3]；…（7分）
（2）由题意可知，当直线L与以M为圆心的单位圆相交于点C，D时，可得k2＞8，且|CD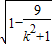|=2
=2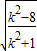令f（k）=
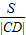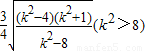=，令t=k2-8（t＞0），则y=
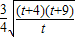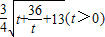=，当且仅当k=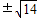取到最小值是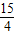所以，
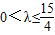…（14分）点评：本题考查直线与圆的位置关系，考查三角形面积的计算，考查基本不等式的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
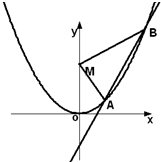
如图，已知直线l：y=kx-2与抛物线C：x2=-2py（p＞0）交于A，B两点，O为坐标原点，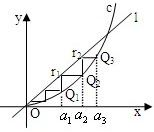
设a＞0，如图，已知直线l：y=ax及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜a）．从C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．
如图，已知直线L：y=kx-1与抛物线C：y=x2，相交于两点A、B，设点M（0，2），△MAB的面积为S．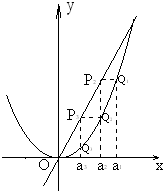
（2013•广州三模）如图，已知直线l：y=4x及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜4）．从曲线C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．