题目内容
通过点A（0，a）的直线y=kx+a与圆（x-2）2+y2=1相交于不同的两点B、C，在线段BC上取一点P，使|BP|：|PC|=|AB|：|AC|，设点B在点C的左边，
（1）试用a和k表示P点的坐标；
（2）求k变化时P点的轨迹；
（3）证明不论a取何值时，上述轨迹恒过圆内的一定点．
（1）试用a和k表示P点的坐标；
（2）求k变化时P点的轨迹；
（3）证明不论a取何值时，上述轨迹恒过圆内的一定点．
（1）设B（x1，y1），c（x2，y2），P（x，y），
依题意知，
=
，
=
，
∴
=
，∴x=
…（4分）
由直线方程代入圆方程，整理得，（1+k2）x2+（2ak-4）x+（a2+3）=0
由x1+x2=
，x1x2=
代入x=
得x=
，y=k
+a=
…（6分）
（2）由x，y的表达式中消去k得2x-ay-3=0，
∴点P的轨迹是直线2x-ay-3=0在圆内的部分．…（8分）
（3）证明：直线2x-ay-3=0恒过定点M（
，0），点M到圆心C（2，0）的距离|MC|=
＜r=1，
∴该点在圆内
∴P点的轨迹恒过圆内的一定点 …（10分）
依题意知，
| |BP| |
| |PC| |
| x-x1 |
| x2-x |
| |AB| |
| |AC| |
| x1 |
| x2 |
∴
| x-x1 |
| x2-x |
| x1 |
| x2 |
| 2x1x2 |
| x1+x2 |
由直线方程代入圆方程，整理得，（1+k2）x2+（2ak-4）x+（a2+3）=0
由x1+x2=
| 4-2ak |
| 1+k2 |
| a2+3 |
| 1+k2 |
| 2x1x2 |
| x1+x2 |
得x=
| a2+3 |
| 2-ak |
| a2+3 |
| 2-ak |
| 3k+2a |
| 2-ak |
（2）由x，y的表达式中消去k得2x-ay-3=0，
∴点P的轨迹是直线2x-ay-3=0在圆内的部分．…（8分）
（3）证明：直线2x-ay-3=0恒过定点M（
| 3 |
| 2 |
| 1 |
| 2 |
∴该点在圆内
∴P点的轨迹恒过圆内的一定点 …（10分）
练习册系列答案
相关题目
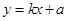与圆
相交于不同的两点B、C，在线段BC上取一点P，使
=
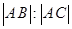，设点B在点C的左边，（1）试用a和k表示P点的坐标；（2）求k变化时P点的轨迹；（3）证明不论a取何值时，上述轨迹恒过圆内的一定点．