摘要：所以当n=0时.菱形ABCD的面积取得最大值.
网址：http://m.1010jiajiao.com/timu_id_530012[举报]
已知椭圆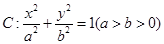
的左、右焦点分别为
、
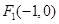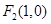，P为椭圆
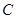上任意一点，且
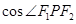的最小值为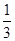
.
（1）求椭圆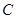的方程；
（2）动圆
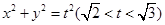与椭圆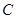相交于A、B、C、D四点，当
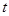为何值时，矩形ABCD的面积取得最大值？并求出其最大面积.
查看习题详情和答案>>
如图，已知半径为r的圆M的内接四边形ABCD的对角线AC和BD相互垂直且交点为P．
（1）若四边形ABCD中的一条对角线AC的长度为d（0＜d＜2r），试求：四边形ABCD面积的最大值；
（2）试探究：当点P运动到什么位置时，四边形ABCD的面积取得最大值，最大值为多少？
（3）对于之前小题的研究结论，我们可以将其类比到椭圆的情形．如图2，设平面直角坐标系中，已知椭圆Γ：
+
=1（a＞b＞0）的内接四边形ABCD的对角线AC和BD相互垂直且交于点P．试提出一个由类比获得的猜想，并尝试给予证明或反例否定．
查看习题详情和答案>>
（1）若四边形ABCD中的一条对角线AC的长度为d（0＜d＜2r），试求：四边形ABCD面积的最大值；
（2）试探究：当点P运动到什么位置时，四边形ABCD的面积取得最大值，最大值为多少？
（3）对于之前小题的研究结论，我们可以将其类比到椭圆的情形．如图2，设平面直角坐标系中，已知椭圆Γ：
| x2 |
| a2 |
| y2 |
| b2 |
已知椭圆C：
+
=1(a＞b＞0)的左、右焦点分别为F1（-1，0）、F2（1，0），P为椭圆C上任意一点，且cos∠F1PF2的最小值为
．
（1）求椭圆C的方程；
（2）动圆x2+y2=t2（
＜t＜
）与椭圆C相交于A、B、C、D四点，当t为何值时，矩形ABCD的面积取得最大值？并求出其最大面积．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
（1）求椭圆C的方程；
（2）动圆x2+y2=t2（
| 2 |
| 3 |
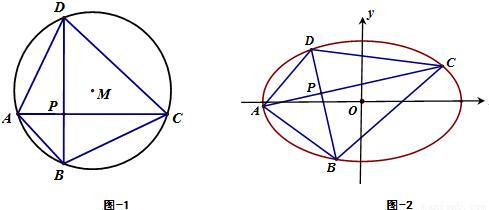
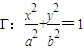（a＞b＞0）的内接四边形ABCD的对角线AC和BD相互垂直且交于点P．试提出一个由类比获得的猜想，并尝试给予证明或反例否定．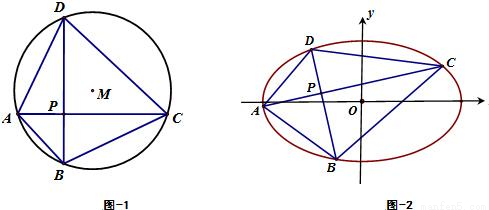
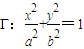（a＞b＞0）的内接四边形ABCD的对角线AC和BD相互垂直且交于点P．试提出一个由类比获得的猜想，并尝试给予证明或反例否定．