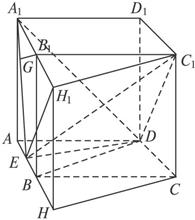
摘要：得所以Rt△AEO∽Rt△BAD.得∠EAO=∠ABD. 所以∠EAO+∠ADF=90° 所以 AF⊥BD.因为 直线AF为直线PA在平面ABCD 内的身影.所以PA⊥BD.[点晴]本小题主要考查棱锥的体积.二面角.异面直线所成的角等知识和空间想象能力.分析问题能力.解题的关键是二面角的使用.使用空间向量能降低对空间想象能力的要求.但坐标系的位置不规则.注意点坐标的表示.
网址：http://m.1010jiajiao.com/timu_id_528971[举报]
（本小题16分）
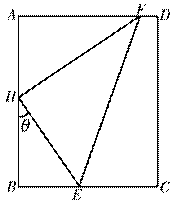某矩形花园
，
,
，
是
的中点，在该花园中有一花圃其形状是以为直角顶点的内接Rt△
，其中E、F分别落在线段
和线段
上如图．分别记
为
，
的周长为
，的面积为
(1)试求的取值范围；
(2)为何值时的值为最小；并求的最小值．
（本小题16分）
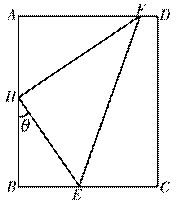某矩形花园
，
,
，
是
的中点，在该花园中有一花圃其形状是以为直角顶点的内接Rt△
，其中E、F分别落在线段
和线段
上如图．分别记
为
，
的周长为
，的面积为
(1)试求的取值范围；
(2)为何值时的值为最小；并求的最小值．
