题目内容
如图,已知直平行六面体ABCD—A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,E为AB的中点,A1E与平面ABCD所成的角为60°.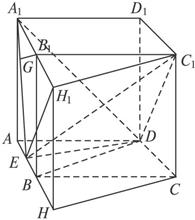
(1)求证:平面A1DE⊥平面ABB1A1;
(2)求点B1到平面A1DE的距离;
(3)求二面角A1-DE-C1的大小.
解法一:(1)证明:连结BD.∵AB=AD,∠BAD=60°,

∴△ABD是正三角形.∵E为AB的中点,∴DE⊥AB.
又在直平行六面体ABCDA1B1C1D1中,AA1⊥平面ABCD,
∵DE![]() 平面ABCD,∴AA1⊥DE.
平面ABCD,∴AA1⊥DE.
∵AA1∩AB=A,∴DE⊥平面ABB1A1.
∵DE![]() 平面A1DE,∴平面A1DE⊥平面ABB1A1.
平面A1DE,∴平面A1DE⊥平面ABB1A1.
(2)解:过点B1作B1G⊥A1E于G点.
∵平面A1DE⊥平面ABB1A1,且平面A1DE∩平面ABB1A1=A1E,
∴B1G⊥平面A1DE,B1G即为点B1到平面A1ED的距离.
∵AA1⊥平面ABCD,∴∠A1EA为A1E与平面ABCD所成的角.
∴∠A1EA=60°.∴∠B1A1G=60°.
在Rt△A1B1G中,B1G=A1B1sin60°=4×![]() ,
,
∴点B1到平面A1ED的距离为2![]() .
.
〔另法提示:可用体积法求点B1到平面A1ED的距离〕
(3)解:分别延长AB、A1B1至H、H1,使BH=B1H1=2,连结CH、C1H1、EH1、HH1.
∵EH=DC,EH∥DC,
∴四边形EHCD为平行四边形.∴ED∥HC.
同理,H1C1∥HC,∴ED∥H1C1.∴E、H1、C1、D四点共面.
由(1)知DE⊥平面ABB1A1,EA1、EH1![]() 平面ABB1A1,
平面ABB1A1,
∴DE⊥EA1,DE⊥EH1.∴∠A1EH1为二面角A1EDC1的平面角.
在Rt△A1AE中,由∠A1EA=60°,AE=2,可得AA1=2![]() ,A1E=4.
,A1E=4.
在Rt△H1HE中,HH1=2![]() ,EH=4,?
,EH=4,?
?∴EH1=2![]() .
.
在△A1EH1中,cos∠A1EH1=![]()
∠A1EH1=arccos![]() .
.
∴二面角A1-ED-C1的大小为arccos![]() .
.
〔另法提示:也可由∠A1EH1=![]() -∠HEH1,得出∠A1EH1=
-∠HEH1,得出∠A1EH1=![]() -arctan
-arctan![]() 〕
〕
解法二:连结BD.∵AB=AD,∠BAD=60°,
∴△ABD是正三角形.
∵E为AB的中点,
∴DE⊥AB,DE=![]() .
.
∴DE⊥DC.
∵AA1⊥平面ABCD,
∴∠A1EA为A1E与平面ABCD所成的角.
∴∠A1EA=60°.又AA1⊥AE,AE=2,
∴A1A=![]() ,A1E=4.
,A1E=4.
(1)证明:以点D为坐标原点,DE、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系,

则E(2![]() ,0,0),C(0,4,0),D1(0,0,2
,0,0),C(0,4,0),D1(0,0,2![]() ),A(2
),A(2![]() ,-2,0),A1(2
,-2,0),A1(2![]() ,-2,23),B(2
,-2,23),B(2![]() ,2,0),B1(2
,2,0),B1(2![]() ,2, 2
,2, 2![]() ),C1(0,4,2
),C1(0,4,2![]() ).
).
∴![]() =(2
=(2![]() ,0,0),
,0,0),![]() =(0,0,2
=(0,0,2![]() ),
),![]() =(0,4,0).
=(0,4,0).
∴![]() =(2
=(2![]() ,0,0)·(0,0,2
,0,0)·(0,0,2![]() )=0,
)=0,
![]() =(2
=(2![]() ,0,0)·(0,4,0)=0.
,0,0)·(0,4,0)=0.
∴![]() .
.
∵AA1∩AB=A,∴DE⊥平面ABB1A1.
∵DE![]() 平面A1DE,∴平面A1DE⊥平面ABB1A1.
平面A1DE,∴平面A1DE⊥平面ABB1A1.
(2)同解法一.
(3)解:由(1)知,DE⊥平面ABB1A1,∴DE⊥平面CDD1C1.
∴DE⊥EA1,DE⊥DC1.
∴〈![]() 〉为二面角A1-ED-C1的平面角.
〉为二面角A1-ED-C1的平面角.
又![]() =(0,-2,2
=(0,-2,2![]() ),
),![]() =(0,4,2
=(0,4,2![]() ),
),
∴![]() =(0,-2,2
=(0,-2,2![]() )·(0,4,2
)·(0,4,2![]() )=4.
)=4.
∴cos〈![]() 〉=
〉= .
.
∴二面角A1-ED-C1的大小为arccos![]() .
.
〔另法提示:本题也可用法向量夹角来求解,但必须根据法向量的方向来说明所求二面角的大小与法向量夹角大小之间的关系〕。

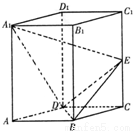
 如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
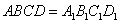 中,
中,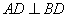 ,
,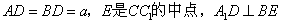
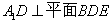 ;
;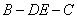 的大小
的大小