题目内容
已知 、
、 是椭圆
是椭圆 的左右焦点,点P是椭圆C上的动点.
的左右焦点,点P是椭圆C上的动点.
(1)若椭圆C的离心率为 ,且
,且 的最大值为8,求椭圆C的方程;
的最大值为8,求椭圆C的方程;
(2)若△ P
P 为等腰直角三角形,求椭圆C的离心率.
为等腰直角三角形,求椭圆C的离心率.
 、
、 是椭圆
是椭圆 的左右焦点,点P是椭圆C上的动点.
的左右焦点,点P是椭圆C上的动点.(1)若椭圆C的离心率为
 ,且
,且 的最大值为8,求椭圆C的方程;
的最大值为8,求椭圆C的方程;(2)若△
 P
P 为等腰直角三角形,求椭圆C的离心率.
为等腰直角三角形,求椭圆C的离心率.解:(1)设椭圆C上的点P坐标为(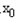 ,
, ),
),
可得 =(﹣c﹣
=(﹣c﹣ ,﹣
,﹣ ),
),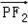 =(c﹣
=(c﹣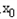 ,﹣
,﹣ ),
),
∴ =(﹣c﹣
=(﹣c﹣ )(c﹣
)(c﹣ )+
)+ =
= +
+ ﹣c2
﹣c2
∵P是椭圆C上的点,满足 =b2(1﹣
=b2(1﹣ ),且﹣a<
),且﹣a< <a
<a
∴ =(1﹣
=(1﹣ )
) +b2﹣c2≤(1﹣
+b2﹣c2≤(1﹣ )a2+b2﹣c2=b2
)a2+b2﹣c2=b2
所以,当且仅当 =a2时,
=a2时, 的最大值为b2=8,可得b=2
的最大值为b2=8,可得b=2
∵椭圆的离心率为 ,
,
∴ ,可得a=
,可得a= c,b=
c,b=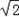 c
c
∴c=2,a=2 ,椭圆C的方程是
,椭圆C的方程是
(2)∵△ P
P 为等腰直角三角形,
为等腰直角三角形,
∴点P为短轴顶点,且OP=
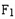
 =c即b=c,
=c即b=c, =c,
=c,
可得a2=2c2,即a= c
c
∴椭圆C的离心率e= =
=
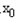 ,
, ),
),可得
 =(﹣c﹣
=(﹣c﹣ ,﹣
,﹣ ),
),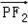 =(c﹣
=(c﹣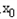 ,﹣
,﹣ ),
),∴
 =(﹣c﹣
=(﹣c﹣ )(c﹣
)(c﹣ )+
)+ =
= +
+ ﹣c2
﹣c2∵P是椭圆C上的点,满足
 =b2(1﹣
=b2(1﹣ ),且﹣a<
),且﹣a< <a
<a∴
 =(1﹣
=(1﹣ )
) +b2﹣c2≤(1﹣
+b2﹣c2≤(1﹣ )a2+b2﹣c2=b2
)a2+b2﹣c2=b2所以,当且仅当
 =a2时,
=a2时, 的最大值为b2=8,可得b=2
的最大值为b2=8,可得b=2
∵椭圆的离心率为
 ,
,∴
 ,可得a=
,可得a= c,b=
c,b=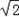 c
c∴c=2,a=2
 ,椭圆C的方程是
,椭圆C的方程是
(2)∵△
 P
P 为等腰直角三角形,
为等腰直角三角形,∴点P为短轴顶点,且OP=

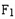
 =c即b=c,
=c即b=c, =c,
=c,可得a2=2c2,即a=
 c
c∴椭圆C的离心率e=
 =
=

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 、
、 是椭圆
是椭圆
 的左右焦点,
的左右焦点, 是
是 上一点,
上一点, ,则
,则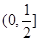 B.
B. C.
C. D.
D. 
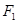 、
、 是椭圆
是椭圆
 的左右焦点,
的左右焦点, 是
是 上一点,
上一点, ,则
,则 B.
B. C.
C. D.
D. 