网址:http://m.1010jiajiao.com/timu_id_523085[举报]
一、选择题
CDABA BCBAB
二、填空题
11. 第二次月考%20%20理科数学.files/image263.gif) 12. -1 13.1<e<2 14.
12. -1 13.1<e<2 14. 第二次月考%20%20理科数学.files/image265.gif) 15.{-1,0}
15.{-1,0}
提示:8.利用点到直线的距离公式知第二次月考%20%20理科数学.files/image267.gif) ,即
,即第二次月考%20%20理科数学.files/image091.gif) 在圆
在圆第二次月考%20%20理科数学.files/image270.gif) 内,也在椭圆
内,也在椭圆第二次月考%20%20理科数学.files/image093.gif) 内,所以过点
内,所以过点第二次月考%20%20理科数学.files/image091.gif) 的直线与椭圆
的直线与椭圆第二次月考%20%20理科数学.files/image093.gif) 总有两个不同的交点.
总有两个不同的交点.
9.可以转化为求第二次月考%20%20理科数学.files/image274.gif) 展开式中所有奇数项系数之和,赋值
展开式中所有奇数项系数之和,赋值第二次月考%20%20理科数学.files/image276.gif) 即可.
即可.
10.原问题第二次月考%20%20理科数学.files/image278.gif) 有且仅有一个正实数解.令
有且仅有一个正实数解.令第二次月考%20%20理科数学.files/image280.gif) ,则
,则第二次月考%20%20理科数学.files/image282.gif) ,令
,令
第二次月考%20%20理科数学.files/image284.gif) ,
,第二次月考%20%20理科数学.files/image286.gif) ,由
,由第二次月考%20%20理科数学.files/image288.gif) 得
得第二次月考%20%20理科数学.files/image290.gif) 或
或第二次月考%20%20理科数学.files/image292.gif) .又
.又第二次月考%20%20理科数学.files/image294.gif) 时,
时,第二次月考%20%20理科数学.files/image296.gif) ;
;第二次月考%20%20理科数学.files/image298.gif) ,
,第二次月考%20%20理科数学.files/image300.gif) 时,
时,第二次月考%20%20理科数学.files/image302.gif) .所以
.所以第二次月考%20%20理科数学.files/image304.gif) .又
.又
第二次月考%20%20理科数学.files/image306.gif) ;
;第二次月考%20%20理科数学.files/image308.gif) .结合三次函数图像即可.
.结合三次函数图像即可.
15. 第二次月考%20%20理科数学.files/image310.gif) ,
,第二次月考%20%20理科数学.files/image312.gif)
第二次月考%20%20理科数学.files/image314.gif) ,即
,即第二次月考%20%20理科数学.files/image316.gif) ,当m为整数时,值为0,m为小数时,值为-1,故所求值域为{-1,0}
,当m为整数时,值为0,m为小数时,值为-1,故所求值域为{-1,0}
三、解答题
16. (1)第二次月考%20%20理科数学.files/image318.gif) …………………3分
…………………3分
由条件第二次月考%20%20理科数学.files/image320.gif) ………………………………………6分
………………………………………6分
(2)第二次月考%20%20理科数学.files/image322.gif) ,令
,令第二次月考%20%20理科数学.files/image324.gif) ,解得
,解得第二次月考%20%20理科数学.files/image326.gif) ,又
,又第二次月考%20%20理科数学.files/image328.gif) 所以
所以第二次月考%20%20理科数学.files/image173.gif) 在
在第二次月考%20%20理科数学.files/image330.gif) 上递减,在
上递减,在第二次月考%20%20理科数学.files/image332.gif) 上递增…………………………13分
上递增…………………………13分
17.(1)答错题目的个数第二次月考%20%20理科数学.files/image334.gif)
第二次月考%20%20理科数学.files/image336.gif)
∴分布列为:第二次月考%20%20理科数学.files/image338.gif) ,期望
,期望第二次月考%20%20理科数学.files/image340.gif) (道题)……7分
(道题)……7分
(2)设该考生会x道题,不会10-x道题,则第二次月考%20%20理科数学.files/image342.gif) …10分
…10分
解得:第二次月考%20%20理科数学.files/image344.gif) 或
或第二次月考%20%20理科数学.files/image346.gif) (舍),故该考生最多会3道题…………………………………13分
(舍),故该考生最多会3道题…………………………………13分
18.(1)作第二次月考%20%20理科数学.files/image348.gif) ,垂足为
,垂足为第二次月考%20%20理科数学.files/image350.gif) ,连结
,连结第二次月考%20%20理科数学.files/image352.gif) ,由题设知,
,由题设知,第二次月考%20%20理科数学.files/image354.gif) 底面
底面第二次月考%20%20理科数学.files/image181.gif) ,
,
且第二次月考%20%20理科数学.files/image350.gif) 为
为第二次月考%20%20理科数学.files/image358.gif) 中点,由
中点,由第二次月考%20%20理科数学.files/image360.gif) 知,
知,第二次月考%20%20理科数学.files/image362.gif) ,
,
从而第二次月考%20%20理科数学.files/image364.gif) ,于是
,于是第二次月考%20%20理科数学.files/image366.gif) ,由三垂线定理知,
,由三垂线定理知,第二次月考%20%20理科数学.files/image193.gif) ……………4分
……………4分
(2)由题意,第二次月考%20%20理科数学.files/image369.gif) ,所以
,所以第二次月考%20%20理科数学.files/image371.gif) 侧面
侧面第二次月考%20%20理科数学.files/image373.gif) ,又
,又第二次月考%20%20理科数学.files/image375.gif) 侧面
侧面第二次月考%20%20理科数学.files/image199.gif) ,所以侧面
,所以侧面第二次月考%20%20理科数学.files/image378.gif) 侧面
侧面第二次月考%20%20理科数学.files/image373.gif) .作
.作第二次月考%20%20理科数学.files/image381.gif) ,垂足为
,垂足为第二次月考%20%20理科数学.files/image383.gif) ,连接
,连接第二次月考%20%20理科数学.files/image385.gif) ,则
,则第二次月考%20%20理科数学.files/image387.gif) 平面
平面第二次月考%20%20理科数学.files/image199.gif) .
.
第二次月考%20%20理科数学.files/image390.jpg) 故
故第二次月考%20%20理科数学.files/image392.gif) 为
为第二次月考%20%20理科数学.files/image197.gif) 与平面
与平面第二次月考%20%20理科数学.files/image199.gif) 所成的角,
所成的角,第二次月考%20%20理科数学.files/image396.gif) …………………………………7分
…………………………………7分
由第二次月考%20%20理科数学.files/image398.gif) ,得:
,得:第二次月考%20%20理科数学.files/image400.gif) , 又
, 又第二次月考%20%20理科数学.files/image402.gif) ,
,
因而第二次月考%20%20理科数学.files/image404.gif) ,所以
,所以第二次月考%20%20理科数学.files/image406.gif) 为等边三角形.
为等边三角形.
作第二次月考%20%20理科数学.files/image408.gif) ,垂足为
,垂足为第二次月考%20%20理科数学.files/image410.gif) ,连结
,连结第二次月考%20%20理科数学.files/image412.gif) .
.
由(1)知,第二次月考%20%20理科数学.files/image414.gif) ,又
,又第二次月考%20%20理科数学.files/image416.gif) ,
,
故第二次月考%20%20理科数学.files/image418.gif) 平面
平面第二次月考%20%20理科数学.files/image420.gif) ,
,第二次月考%20%20理科数学.files/image422.gif) ,
,
第二次月考%20%20理科数学.files/image424.gif) 是二面角
是二面角第二次月考%20%20理科数学.files/image426.gif) 的平面角………………………………………………...10分
的平面角………………………………………………...10分
第二次月考%20%20理科数学.files/image428.gif) .
.第二次月考%20%20理科数学.files/image430.gif) ,
,第二次月考%20%20理科数学.files/image432.gif) ,
,第二次月考%20%20理科数学.files/image434.gif) ,
,
所以二面角第二次月考%20%20理科数学.files/image436.gif) 为
为第二次月考%20%20理科数学.files/image438.gif) 或
或第二次月考%20%20理科数学.files/image440.gif) ……………………….13分
……………………….13分
19.(1)由第二次月考%20%20理科数学.files/image442.gif) ,得
,得第二次月考%20%20理科数学.files/image444.gif) ,
,第二次月考%20%20理科数学.files/image446.gif) …2分
…2分
又第二次月考%20%20理科数学.files/image215.gif) ,
,第二次月考%20%20理科数学.files/image448.gif)
第二次月考%20%20理科数学.files/image450.gif) 两式相减,得:
两式相减,得:
第二次月考%20%20理科数学.files/image452.gif) ,
,第二次月考%20%20理科数学.files/image454.gif)
第二次月考%20%20理科数学.files/image450.gif)
综上,数列第二次月考%20%20理科数学.files/image209.gif) 为首项为1,公比为
为首项为1,公比为第二次月考%20%20理科数学.files/image457.gif) 的等比数列…………………………..…….6分
的等比数列…………………………..…….6分
(2)由第二次月考%20%20理科数学.files/image459.gif) ,得
,得第二次月考%20%20理科数学.files/image461.gif) ,所以
,所以第二次月考%20%20理科数学.files/image223.gif) 是首项为1,,公差为
是首项为1,,公差为第二次月考%20%20理科数学.files/image177.gif) 的等差数列,
的等差数列,第二次月考%20%20理科数学.files/image465.gif) ……………………………….…………………………....9分
……………………………….…………………………....9分
第二次月考%20%20理科数学.files/image229.gif)
第二次月考%20%20理科数学.files/image467.gif)
第二次月考%20%20理科数学.files/image469.gif)
第二次月考%20%20理科数学.files/image471.gif) ……………………….………………………....13分
……………………….………………………....13分
20.(1)设点第二次月考%20%20理科数学.files/image473.gif) ,则
,则第二次月考%20%20理科数学.files/image475.gif)
第二次月考%20%20理科数学.files/image477.gif)
所以,当x=p时,第二次月考%20%20理科数学.files/image479.gif) …………………………………………………….….4分
…………………………………………………….….4分
(2)由条件,设直线第二次月考%20%20理科数学.files/image481.gif) ,代入
,代入第二次月考%20%20理科数学.files/image483.gif) ,得:
,得:第二次月考%20%20理科数学.files/image485.gif)
设第二次月考%20%20理科数学.files/image487.gif) ,则
,则第二次月考%20%20理科数学.files/image489.gif) ,
,
第二次月考%20%20理科数学.files/image491.gif) …......................................................................................7分
…......................................................................................7分
第二次月考%20%20理科数学.files/image493.gif) ….10分
….10分
又第二次月考%20%20理科数学.files/image495.gif) ,所以
,所以第二次月考%20%20理科数学.files/image237.gif) 为定值2……………………………………………….12分
为定值2……………………………………………….12分
21. (1)第二次月考%20%20理科数学.files/image497.gif) 是奇函数,则
是奇函数,则第二次月考%20%20理科数学.files/image499.gif) 恒成立,
恒成立,
第二次月考%20%20理科数学.files/image501.gif)
第二次月考%20%20理科数学.files/image503.gif) ,
,第二次月考%20%20理科数学.files/image501.gif)
第二次月考%20%20理科数学.files/image506.gif) ,故
,故第二次月考%20%20理科数学.files/image508.gif) …………………….2分
…………………….2分
(2)第二次月考%20%20理科数学.files/image510.gif) 在
在第二次月考%20%20理科数学.files/image251.gif) 上单调递减,
上单调递减,第二次月考%20%20理科数学.files/image513.gif) ,
,第二次月考%20%20理科数学.files/image515.gif) ,
,
第二次月考%20%20理科数学.files/image501.gif) 只需
只需第二次月考%20%20理科数学.files/image518.gif)
第二次月考%20%20理科数学.files/image520.gif)
第二次月考%20%20理科数学.files/image522.gif)
第二次月考%20%20理科数学.files/image524.gif) (
(第二次月考%20%20理科数学.files/image526.gif) 恒成立.
恒成立.
令第二次月考%20%20理科数学.files/image528.gif) ,则
,则第二次月考%20%20理科数学.files/image530.gif)
第二次月考%20%20理科数学.files/image532.gif)
第二次月考%20%20理科数学.files/image534.gif) ,而
,而第二次月考%20%20理科数学.files/image536.gif) 恒成立,
恒成立,第二次月考%20%20理科数学.files/image538.gif) .….…………………….7分
.….…………………….7分
(3)由(1)知第二次月考%20%20理科数学.files/image540.gif) ,
,第二次月考%20%20理科数学.files/image501.gif) 方程为
方程为第二次月考%20%20理科数学.files/image543.gif) ,
,
令第二次月考%20%20理科数学.files/image545.gif) ,
,第二次月考%20%20理科数学.files/image547.gif) ,
, 第二次月考%20%20理科数学.files/image549.gif) ,
,
当第二次月考%20%20理科数学.files/image551.gif) 时,
时,第二次月考%20%20理科数学.files/image553.gif) ,
,第二次月考%20%20理科数学.files/image555.gif) 在
在第二次月考%20%20理科数学.files/image557.gif) 上为增函数;
上为增函数;
当第二次月考%20%20理科数学.files/image559.gif) 时,
时,第二次月考%20%20理科数学.files/image561.gif) ,
,第二次月考%20%20理科数学.files/image555.gif) 在
在第二次月考%20%20理科数学.files/image564.gif) 上为减函数;
上为减函数;
第二次月考%20%20理科数学.files/image566.gif) 当
当第二次月考%20%20理科数学.files/image568.gif) 时,
时,第二次月考%20%20理科数学.files/image570.gif) .而
.而第二次月考%20%20理科数学.files/image572.gif) ,
,
函数第二次月考%20%20理科数学.files/image574.gif) 、
、第二次月考%20%20理科数学.files/image576.gif) 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
第二次月考%20%20理科数学.files/image501.gif) 当
当第二次月考%20%20理科数学.files/image579.gif) 即
即第二次月考%20%20理科数学.files/image581.gif)
第二次月考%20%20理科数学.files/image583.gif) 时,方程无解;
时,方程无解;
当第二次月考%20%20理科数学.files/image585.gif) ,即
,即第二次月考%20%20理科数学.files/image587.gif) 时,方程有一个根;
时,方程有一个根;
当第二次月考%20%20理科数学.files/image589.gif) ,
,第二次月考%20%20理科数学.files/image532.gif) 即
即第二次月考%20%20理科数学.files/image591.gif) 时,方程有两个根.………………………………….12分
时,方程有两个根.………………………………….12分
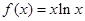 .
.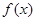 的单调递减区间;
的单调递减区间;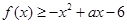 在
在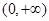 上恒成立,求实数
上恒成立,求实数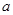 的取值范围;
的取值范围; 作函数
作函数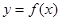 图像的切线,求切线方程
图像的切线,求切线方程 .
. 的单调递减区间;
的单调递减区间;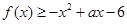 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; 作函数
作函数 图像的切线,求切线方程
图像的切线,求切线方程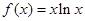 .
.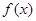 的单调递减区间;
的单调递减区间;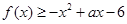 在
在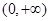 上恒成立,求实数
上恒成立,求实数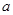 的取值范围;
的取值范围;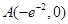 作函数
作函数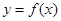 图像的切线,求切线方程
图像的切线,求切线方程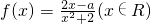 在区间[-1,1]上是增函数
在区间[-1,1]上是增函数 的两个非零实根为x1,x2.
的两个非零实根为x1,x2.