题目内容
已知![]() 在区间
在区间![]() 上是增函数
上是增函数
(I)求实数![]() 的取值范围;
的取值范围;
(II)记实数![]() 的取值范围为集合A,且设关于
的取值范围为集合A,且设关于![]() 的方程
的方程![]() 的两个非零实根为
的两个非零实根为![]() 。
。
①求![]() 的最大值;
的最大值;
②试问:是否存在实数m,使得不等式![]() 对
对![]() 及
及![]() 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(I)![]() 的取值范围为
的取值范围为![]()
(II)存在实数![]() 满足题设条件
满足题设条件
解析:
1.解:(1)![]() ……………………………………………1分
……………………………………………1分
![]() 在
在![]() 上是增函数
上是增函数
![]() 即
即![]() ,在
,在![]() 恒成立 …………① …………3分
恒成立 …………① …………3分
设 ![]() ,则由①得
,则由①得
![]() 解得
解得![]()
所以,![]() 的取值范围为
的取值范围为![]() ………………………………………………………6分
………………………………………………………6分
(2)由(1)可知![]()
由![]() 即
即![]() 得
得![]()
![]()
![]() 是方程
是方程![]() 的两个非零实根
的两个非零实根
![]() ,
,![]() ,又由
,又由![]()
![]() ……………………………9分
……………………………9分
于是要使![]() 对
对![]() 及
及![]() 恒成立
恒成立
即![]() 即
即![]() 对
对![]() 恒成立 ………②………11分
恒成立 ………②………11分
![]() 设
设 ![]() ,则由②得
,则由②得
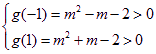 解得
解得![]() 或
或![]()
故存在实数![]() 满足题设条件…………………………14分
满足题设条件…………………………14分

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 在区间
在区间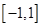 上是增函数.
上是增函数. 的值组成的集合
的值组成的集合 ;
;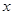 的方程
的方程 的两个非零实根为
的两个非零实根为 、
、 .试问:是否存在实数
.试问:是否存在实数 ,使得不等式
,使得不等式 对任意
对任意 及
及 恒成立?若存在,求
恒成立?若存在,求 在区间
在区间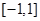 上是增函数,则
上是增函数,则 的取值范围为(
)
的取值范围为(
)  B、
B、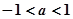
 D、不存在
D、不存在 在区间
在区间 上是增函数.
上是增函数. 的值组成的集合
的值组成的集合 ;
; 的方程
的方程 的两个非零实根为
的两个非零实根为 ,试问:是否存在实数
,试问:是否存在实数 ,使得不等式
,使得不等式 对任意
对任意 及
及 恒成立?若存在,求
恒成立?若存在,求 在区间
在区间 上是增函数,则实数
上是增函数,则实数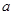 的范围是( )
的范围是( ) B.
B.  C.
C.  D.
D. 