摘要：(2)当n≥2时.an=f()=.
网址：http://m.1010jiajiao.com/timu_id_52082[举报]
设f（x）=
（a＞0）为奇函数，且|f（x）|min=2
，数列{an}与{bn}满足如下关系：a1=2，an+1=
，bn=
．
（1）求f（x）的解析表达式；
（2）证明：当n∈N+时，有bn≤(
)n．
查看习题详情和答案>>
| ax2+bx+1 |
| x+c |
| 2 |
| f(an)-an |
| 2 |
| an-1 |
| an+1 |
（1）求f（x）的解析表达式；
（2）证明：当n∈N+时，有bn≤(
| 1 |
| 3 |
设f（x）=x2，g（x）=8x，数列{an}（n∈N*）满足a1=2，（an+1-an）•g（an-1）+f（an-1）=0，记bn=
(n+1)(an-1)．（Ⅰ）求证：数列{an-1}是等比数列；
（Ⅱ）当n为何值时，bn取最大值，并求此最大值；（Ⅲ）求数列{bn}的前n项和Sn． 查看习题详情和答案>>
| 7 | 8 |
（Ⅱ）当n为何值时，bn取最大值，并求此最大值；（Ⅲ）求数列{bn}的前n项和Sn． 查看习题详情和答案>>
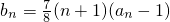．（Ⅰ）求证：数列{an-1}是等比数列；