题目内容
设f(x)=x2,g(x)=8x,数列{an}(n∈N*)满足a1=2,(an+1-an)•g(an-1)+f(an-1)=0,记bn=
(n+1)(an-1).(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)当n为何值时,bn取最大值,并求此最大值;(Ⅲ)求数列{bn}的前n项和Sn.
| 7 |
| 8 |
(Ⅱ)当n为何值时,bn取最大值,并求此最大值;(Ⅲ)求数列{bn}的前n项和Sn.
(Ⅰ)由已知,得(an+1-an)•8(an-1)+(an-1)2=0.
即(an-1)(8an+1-7an-1)=0.
∵a1=2≠1,∴a2≠1,同理a3≠1,…,an≠1.
∴8an+1=7an+1.
即8(an+1-1)=7(an-1),
∴数列{an-1}是以a1-1=1为首项,
为公比的等比数列.
(Ⅱ)由(1),得an-1=(
)n-1.
∴bn=(n+1)•(
)n.
则bn+1=(n+2)•(
)n+1.
∵
=
•
,设
≥1,则n≤6.
因此,当n<6时,bn<bn+1;当n=6时,b6=b7,当n>6时,bn>bn+1.
∴当n=6或7时,bn取得最大值.
(Ⅲ)Sn=2•
+3•(
)2+4•(
)3+…+n•(
)n-1+(n+1)•(
)n
•Sn=2•(
)2+3•(
)3+4•(
)4+…+n•(
)n+(n+1)•(
)n+1
相减得:
•Sn=2•
+(
)2+(
)3+…+(
)n-(n+1)•(
)n+1=
+
×8×[1-(
)n]-(n+1)•(
)n+1
=
-(n+9)•(
)n+1
∴Sn=63-8(n+9)•(
)n+1.
即(an-1)(8an+1-7an-1)=0.
∵a1=2≠1,∴a2≠1,同理a3≠1,…,an≠1.
∴8an+1=7an+1.
即8(an+1-1)=7(an-1),
∴数列{an-1}是以a1-1=1为首项,
| 7 |
| 8 |
(Ⅱ)由(1),得an-1=(
| 7 |
| 8 |
∴bn=(n+1)•(
| 7 |
| 8 |
则bn+1=(n+2)•(
| 7 |
| 8 |
∵
| bn+1 |
| bn |
| n+2 |
| n+1 |
| 7 |
| 8 |
| bn+1 |
| bn |
因此,当n<6时,bn<bn+1;当n=6时,b6=b7,当n>6时,bn>bn+1.
∴当n=6或7时,bn取得最大值.
(Ⅲ)Sn=2•
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
相减得:
| 1 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
=
| 63 |
| 8 |
| 7 |
| 8 |
∴Sn=63-8(n+9)•(
| 7 |
| 8 |

练习册系列答案
相关题目
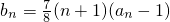 .(Ⅰ)求证:数列{an-1}是等比数列;
.(Ⅰ)求证:数列{an-1}是等比数列;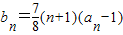 .(Ⅰ)求证:数列{an-1}是等比数列;
.(Ⅰ)求证:数列{an-1}是等比数列;