摘要:解法一,
网址:http://m.1010jiajiao.com/timu_id_516639[举报]

 (理)已知函数f(x)=
(理)已知函数f(x)=| ln(2-x2) |
| |x+2|-2 |
(1)试判断f(x)的奇偶性并给予证明;
(2)求证:f(x)在区间(0,1)单调递减;
(3)如图给出的是与函数f(x)相关的一个程序框图,试构造一个公差不为零的等差数列
{an},使得该程序能正常运行且输出的结果恰好为0.请说明你的理由.
(文)如图,在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
(1)求证:F<0;
(2)若四边形ABCD的面积为8,对角线AC的长为2,且
| AB |
| AD |
(3)设四边形ABCD的一条边CD的中点为G,OH⊥AB且垂足为H.试用平面解析几何的研究方法判
断点O、G、H是否共线,并说明理由. 查看习题详情和答案>>
(理)如图展示了一个由区间(0,1)到实数集R的对应过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图3.图③中直线AM与x轴交于点N(n,0),则m对应n,记作f(m)=n.给出下列结论:

(1)方程f(x)=0的解是x=
;
(2)f(
)=1;
(3)f(x)是奇函数;
(4)f(x)在定义域上单调递增;
(5)f(x)的图象关于点(
,0)对称.
上述说法中正确命题的序号是
查看习题详情和答案>>

(1)方程f(x)=0的解是x=
| 1 |
| 2 |
(2)f(
| 1 |
| 4 |
(3)f(x)是奇函数;
(4)f(x)在定义域上单调递增;
(5)f(x)的图象关于点(
| 1 |
| 2 |
上述说法中正确命题的序号是
(1)(4)(5)
(1)(4)(5)
(填出所有正确命题的序号)(理)已知等差数列 的公差是
的公差是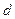 ,
, 是该数列的前
是该数列的前 项和.
项和.
(1)试用 表示
表示 ,其中
,其中 、
、 均为正整数;
均为正整数;
(2)利用(1)的结论求解:“已知
 ,求
,求 ”;
”;
(3)若数列 前
前 项的和分别为
项的和分别为
 ,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列
,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列 的前
的前 项和
项和 ,前
,前 项和
项和 ,求数列
,求数列 的前2010项的和
的前2010项的和 .”
.”

 ;
;  ;
; 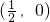 对称.
对称.
 (理)已知函数
(理)已知函数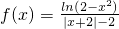 .
.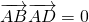 ,求D2+E2-4F的值;
,求D2+E2-4F的值;