摘要:(Ⅱ)设直线过点且与轨迹有两个不同的交点求直线的斜率的取值范围,
网址:http://m.1010jiajiao.com/timu_id_515237[举报]
(2013•石家庄二模)在平面直角坐标系中,已知点F(0,1),直线l:y=-1,P为平面内动点,过点P作直线l的垂线,垂足为Q,且
•(
+
)=0.
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)过点M(0,m)(m>0)的直线AB与曲线E交于A、B两个不同点,设∠AFB=θ,若对于所有这样的直线AB,都有θ∈(
,π].求m的取值范围.
查看习题详情和答案>>
| QF |
| QP |
| FP |
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)过点M(0,m)(m>0)的直线AB与曲线E交于A、B两个不同点,设∠AFB=θ,若对于所有这样的直线AB,都有θ∈(
| π |
| 2 |
已知点P为圆周x2+y2=4的动点,过P点作PH⊥x轴,垂足为H,设线段PH的中点为E,记点E的轨迹方程为C,点A(0,1)
(1)求动点E的轨迹方程C;
(2)若斜率为k的直线l经过点A(0,1)且与曲线C的另一个交点为B,求△OAB面积的最大值及此时直线l的方程;
(3)是否存在方向向量
=(1,k)(k≠0)的直线l,使得l与曲线C交与两个不同的点M,N,且有|
|=|
|?若存在,求出k的取值范围;若不存在,说明理由.
查看习题详情和答案>>
(1)求动点E的轨迹方程C;
(2)若斜率为k的直线l经过点A(0,1)且与曲线C的另一个交点为B,求△OAB面积的最大值及此时直线l的方程;
(3)是否存在方向向量
| a |
| AM |
| AN |
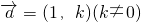 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有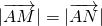 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由. 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有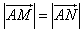 ?若存在,求出k的取值范围;若不存在,说明理由。
?若存在,求出k的取值范围;若不存在,说明理由。  的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有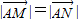 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由.