摘要:一等差数列.根据等差数列求和公式得:.即.解
网址:http://m.1010jiajiao.com/timu_id_514208[举报]
已知等差数列![]() 中,
中,![]() ,
,![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.![]()
(1)求![]() 的通项公式;
的通项公式;
(2)求证:![]() ;
;
(3)通过对数列![]() 的探究,写出“
的探究,写出“![]() 成等比数列”的一个真命题并说明理由(
成等比数列”的一个真命题并说明理由(![]() ,
,![]() ).
).
说明:对于第(3)题,将根据对问题探究的完整性,给予不同的评分.
查看习题详情和答案>>
(理)已知等差数列{an}中,a3=7,a1+a2+a3=12,令bn=anan+1,数列{
}的前n项和为Tn.n∈N*.
(1)求{an}的通项公式;
(2)求证:Tn<
;
(3)通过对数列{Tn}的探究,写出“T1,Tm,Tn成等比数列”的一个真命题并说明理由(1<m<n,m,n∈N*).
说明:对于第(3)题,将根据对问题探究的完整性,给予不同的评分. 查看习题详情和答案>>
| 1 |
| bn |
(1)求{an}的通项公式;
(2)求证:Tn<
| 1 |
| 3 |
(3)通过对数列{Tn}的探究,写出“T1,Tm,Tn成等比数列”的一个真命题并说明理由(1<m<n,m,n∈N*).
说明:对于第(3)题,将根据对问题探究的完整性,给予不同的评分. 查看习题详情和答案>>
定义:如果数列{an}的任意连续三项均能构成一个三角形的三边长,则称{an}为“三角形”数列.对于“三角形”数列{an},如果函数y=f(x)使得bn=f(an)仍为一个“三角形”数列,则称y=f(x)是数列{an}的“保三角形函数”,(n∈N﹡).
(1)已知{an}是首项为2,公差为1的等差数列,若f(x)=kx,(k>1)是数列{an}的“保三角形函数”,求k的取值范围;
(2)已知数列{cn}的首项为2010,Sn是数列{cn}的前n项和,且满足4Sn+1-3Sn=8040,证明{cn}是“三角形”数列;
(3)[文科]若g(x)=lgx是(2)中数列{cn}的“保三角形函数”,问数列{cn}最多有多少项.
[理科]根据“保三角形函数”的定义,对函数h(x)=-x2+2x,x∈[1,A],和数列1,1+d,1+2d,(d>0)提出一个正确的命题,并说明理由. 查看习题详情和答案>>
(1)已知{an}是首项为2,公差为1的等差数列,若f(x)=kx,(k>1)是数列{an}的“保三角形函数”,求k的取值范围;
(2)已知数列{cn}的首项为2010,Sn是数列{cn}的前n项和,且满足4Sn+1-3Sn=8040,证明{cn}是“三角形”数列;
(3)[文科]若g(x)=lgx是(2)中数列{cn}的“保三角形函数”,问数列{cn}最多有多少项.
[理科]根据“保三角形函数”的定义,对函数h(x)=-x2+2x,x∈[1,A],和数列1,1+d,1+2d,(d>0)提出一个正确的命题,并说明理由. 查看习题详情和答案>>
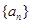 是一个等差数列,且
是一个等差数列,且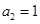 ,
, 。
。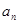 ;
;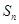 的最大值.
的最大值.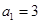 ,
,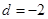 ,求
,求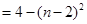 ,求最大项。
,求最大项。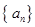 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称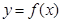 使得
使得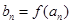 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称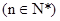 .
.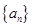 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若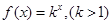 是数列
是数列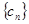 的首项为2010,
的首项为2010,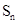 是数列
是数列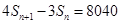 ,证明
,证明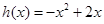 ,
,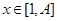 ,和数列1,
,和数列1,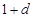 ,
,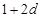 ,(
,(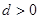 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.