题目内容
已知等差数列![]() 中,
中,![]() ,
,![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.![]()
(1)求![]() 的通项公式;
的通项公式;
(2)求证:![]() ;
;
(3)通过对数列![]() 的探究,写出“
的探究,写出“![]() 成等比数列”的一个真命题并说明理由(
成等比数列”的一个真命题并说明理由(![]() ,
,![]() ).
).
说明:对于第(3)题,将根据对问题探究的完整性,给予不同的评分.
同下
解析:
(1)设数列![]() 的公差为
的公差为![]() ,由
,由![]() ,
,![]() .
.
解得![]() ,
,![]() =3 ∴
=3 ∴![]() .
. ![]() ……4分
……4分
(2) ![]()
∴![]() ∴
∴![]() ;8分
;8分
(3)由(2)知,![]() ∴
∴![]() ,
,![]()
若![]() 成等比数列,则
成等比数列,则![]() 即
即![]() .……10分
.……10分
以下6分按3个层次评分
第一层次满分3分:
例如:因为![]() ,所以只有满足
,所以只有满足![]() 的大于1的正整数
的大于1的正整数![]() ,才有可能使得
,才有可能使得![]() 成立 ……13分
成立 ……13分
或者取具体数值探究如:
当![]() 时,
时,![]()
![]() ,
,![]() =16,符合题意;
=16,符合题意;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解;
无正整数解;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解;
无正整数解;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解;
无正整数解;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解; ……13分
无正整数解; ……13分
或者描述性说明,如:
因为![]() ,
,![]() ,所以只有当
,所以只有当![]() 取值较小时,才有可能使得
取值较小时,才有可能使得![]() 成立 ……13分
成立 ……13分
第二层次3+2分:
在第一层次的基础上继续探究,并明确指出:当正整数m=2,n=16时,![]() 成等比数列. 如:
成等比数列. 如:
不等式![]() 即
即![]() ,解得
,解得![]() ,所以
,所以![]() (舍去),
(舍去),![]() 。当
。当![]() 时,
时,![]()
![]() ,
,![]() =16,符合题意;所以当正整数m=2,n=16时,
=16,符合题意;所以当正整数m=2,n=16时,![]() 成等比数列. ……15分
成等比数列. ……15分
(注:![]() )
)
或者如:当![]() 时,
时,![]() ,则
,则![]() ,而
,而![]() ,所以,此时不存在正整数m,n,且1<m<n,使得
,所以,此时不存在正整数m,n,且1<m<n,使得![]() 成等比数列.所以当正整数m=2,n=16时,
成等比数列.所以当正整数m=2,n=16时,![]() 成等比数列. ……15分
成等比数列. ……15分
第三层次5+1分:
在前面探索的基础上,写出“![]() 成等比数列”的真命题:当且仅当正整数m=2,n=16时,
成等比数列”的真命题:当且仅当正整数m=2,n=16时,![]() 成等比数列. ……16分
成等比数列. ……16分
(说明:对问题探究的完整性体现在过程中即可)

练习册系列答案
相关题目
 中,
中, 的值是( )
的值是( ) B.
B.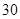 C.
C.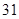 D.
D.
 中,
中, 的值是 (
)
的值是 (
)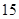 B.
B.
 C.
31 D. 64
C.
31 D. 64 }中,
}中, ,设
,设 求:
求: .
. 中,
中, ,记
,记 ,则
,则 的值为( )
的值为( )