摘要:(1)求的单调递减区间(用表示),
网址:http://m.1010jiajiao.com/timu_id_512939[举报]
已知函数 在
在 取得极值
取得极值
(1)求 的单调区间(用
的单调区间(用 表示);
表示);
(2)设 ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问利用

根据题意 在
在 取得极值,
取得极值, 
对参数a分情况讨论,可知
当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

第二问中, 由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在


从而求解。
解: 
 …..3分
…..3分
 在
在 取得极值,
取得极值,  ……………………..4分
……………………..4分
(1) 当 即
即 时 递增区间:
时 递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,
 ………….6分
………….6分
(2)  由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在

 ……………….10分
……………….10分
 , 使
, 使 成立
成立



 得:
得: 
查看习题详情和答案>>
已知函数![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]() ,其中
,其中![]() 、
、![]() 、
、![]() 为常数.
为常数.
(1)函数![]() 是否存在单调递减区间?若存在,则求出单调递减区间(用
是否存在单调递减区间?若存在,则求出单调递减区间(用![]() 表示);
表示);
(2)若![]() 不是函数
不是函数![]() 的极值点,求证:函数
的极值点,求证:函数![]() 的图像关于点
的图像关于点![]() 对称.
对称.
设函数 定义域为
定义域为 ,且
,且 .
.
设点 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 分别作直线
分别作直线 和
和 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.

(1)写出 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)
(2)设点 的横坐标
的横坐标 ,求
,求 点的坐标(用
点的坐标(用 的代数式表示);(7分)
的代数式表示);(7分)
(3)设 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.(7分)
面积的最小值.(7分)
查看习题详情和答案>>
 定义域为
定义域为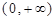 ,且
,且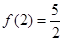 .
.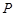 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点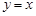 和
和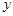 轴的垂线,垂足分别为
轴的垂线,垂足分别为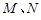 .
.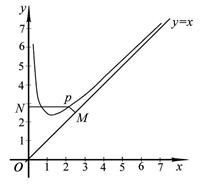
 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)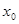 ,求
,求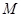 点的坐标(用
点的坐标(用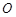 为坐标原点,求四边形
为坐标原点,求四边形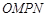 面积的最小值.(7分)
面积的最小值.(7分) 设函数
设函数