摘要：21．对数列{an}.规定{△an}为数列{an}的一阶差分数列.其中△an=an+1-an．对自然数k.规定{△kan}为{an}的k阶差分数列.其中△kan=△k-1an+1-△k-1an=△(△k-1an)．(1)已知数列{an}的通项公式an=n2+n (n∈N).试判断{△an}.{△2an}是否为等差或等比数列.为什么?
网址：http://m.1010jiajiao.com/timu_id_510300[举报]
（本小题满分12分）已知单调递增的等比数列｛an｝满足：a2+a3+a4=28,且a3+2是a2,a4的等差中项。
（1）求数列｛an｝的通项公式；
（2）若bn=
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立，试求m的取值范围。
（本小题满分12分）
已知单调递增的等比数
列｛an｝满足：a2+a3+a4=28,且a3+2是a2,a4的等差中项。
（1）求数列｛an｝的通项公式;
（2）若b
n=
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
（本小题满分12分）已知数列｛an｝的前n项和为Sn，且
（n
）．数列｛bn｝是等差数列，且
，
．
(Ⅰ)求数列｛an｝的通项公式；
(Ⅱ)求数列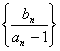
的前n项和Tn；若不等式
（a>0且a≠1）对一切n 恒成立，求实数x的取值范围．
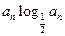,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立，试求m的取值范围。
列｛an｝满足：a2+a3+a4=28,且a3+2是a2,a4的等差中项。
n=
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。