题目内容
（本小题满分12分）已知单调递增的等比数列｛an｝满足：a2+a3+a4=28,且a3+2是a2,a4的等差中项。
（1）求数列｛an｝的通项公式；
（2）若bn=
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立，试求m的取值范围。
（1）
（2）
解析:
（1）设等比数列
的首项为
，公比为q。
依题意，有
代入a2+a3+a4=28，得
┉┉┉┉┉┉┉┉2分
∴
∴
解之得
或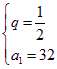
┉┉┉┉┉┉┉┉4分
又单调递增，∴
∴ ┉┉┉┉┉┉┉┉6分
（2）
∴
①
∴
②
∴①-②得
＝
┉┉┉┉┉┉┉┉9分
由sn+(n+m)an+1<0，
即
对任意正整数n恒成立，
∴
。
对任意正数
恒成立，┉┉┉┉┉┉┉┉11分
∵
即m的取值范围是。┉┉┉┉┉┉┉┉13分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
