摘要:的条件下.若.证明直线过定点.并求出这个定点的坐标.
网址:http://m.1010jiajiao.com/timu_id_505355[举报]
已知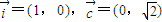 ,若过定点
,若过定点 、以
、以 (λ∈R)为法向量的直线l1与过点
(λ∈R)为法向量的直线l1与过点 以
以 为法向量的直线l2相交于动点P.
为法向量的直线l2相交于动点P.
(1)求直线l1和l2的方程;
(2)求直线l1和l2的斜率之积k1k2的值,并证明必存在两个定点E,F,使得 恒为定值;
恒为定值;
(3)在(2)的条件下,若M,N是 上的两个动点,且
上的两个动点,且 ,试问当|MN|取最小值时,向量
,试问当|MN|取最小值时,向量 与
与 是否平行,并说明理由.
是否平行,并说明理由.
查看习题详情和答案>>
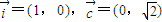 ,若过定点
,若过定点 、以
、以 (λ∈R)为法向量的直线l1与过点
(λ∈R)为法向量的直线l1与过点 以
以 为法向量的直线l2相交于动点P.
为法向量的直线l2相交于动点P.(1)求直线l1和l2的方程;
(2)求直线l1和l2的斜率之积k1k2的值,并证明必存在两个定点E,F,使得
 恒为定值;
恒为定值;(3)在(2)的条件下,若M,N是
 上的两个动点,且
上的两个动点,且 ,试问当|MN|取最小值时,向量
,试问当|MN|取最小值时,向量 与
与 是否平行,并说明理由.
是否平行,并说明理由.查看习题详情和答案>>
 设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=
设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=
| ||
| 3 |
(1)证明{rn}为等比数列(提示:
| rn |
| λn |
| ||
| 3 |
(2)设r1=1,求数列{
| n |
| rn |
(3)在(2)的条件下,若对任意的正整数n恒有不等式Sn>
| 9 |
| 4 |
| an |
| rn |
已知函数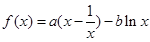 (
(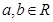 ),
),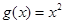 .
.
(Ⅰ)若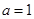 ,曲线
,曲线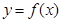 在点
在点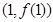 处的切线与
处的切线与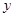 轴垂直,求
轴垂直,求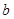 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求证: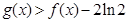 ;
;
(Ⅲ)若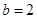 ,试探究函数
,试探究函数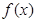 与
与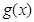 的图象在其公共点处是否存在公切线,若存在,研究
的图象在其公共点处是否存在公切线,若存在,研究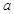 值的个数;若不存在,请说明理由.
值的个数;若不存在,请说明理由.
查看习题详情和答案>>
 (
( ),
), .
. ,曲线
,曲线 在点
在点 处的切线与
处的切线与 轴垂直,求
轴垂直,求 的值;
的值; ;
; ,试探究函数
,试探究函数 与
与 的图象在其公共点处是否存在公切线,若存在,研究
的图象在其公共点处是否存在公切线,若存在,研究 值的个数;若不存在,请说明理由.
值的个数;若不存在,请说明理由.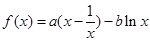 (
(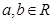 ),
),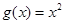 .
.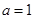 ,曲线
,曲线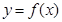 在点
在点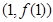 处的切线与
处的切线与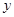 轴垂直,求
轴垂直,求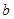 的值;
的值;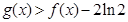 ;
;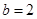 ,试探究函数
,试探究函数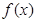 与
与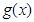 的图象在其公共点处是否存在公切线,若存在,研究
的图象在其公共点处是否存在公切线,若存在,研究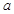 值的个数;若不存在,请说明理由.
值的个数;若不存在,请说明理由.