摘要:(1)记三次摸奖恰有一次中奖的概率为.试问当n等于多少时.的值最大?的条件下.将5个白球全部取出后.对剩下的n个红球全部作如下标记:记上i号的有i个.其余的红球记上0号.现从袋中任取一球.ξ表示所取球的标号.求ξ的分布列.期望和方差.
网址:http://m.1010jiajiao.com/timu_id_504723[举报]
(本小题满分12分)
一个口袋中装有大小相同的 个红球(
个红球( 且
且 )和
)和 个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
(Ⅰ)试用 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率 ;
;
(Ⅱ)记从口袋中三次摸奖(每次摸奖后放回)恰有一次中奖的概率为 ,求
,求 的最大值?
的最大值?
(Ⅲ)在(Ⅱ)的条件下,将 个白球全部取出后,对剩下的
个白球全部取出后,对剩下的 个红球全部作如下标记:记上
个红球全部作如下标记:记上 号的有
号的有 个(
个( ),其余的红球记上
),其余的红球记上 号,现从袋中任取一球。
号,现从袋中任取一球。 表示所取球的标号,求
表示所取球的标号,求 的分布列、期望和方差。
的分布列、期望和方差。
查看习题详情和答案>>
(本小题满分14分)一个口袋中装有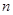 个红球
个红球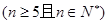 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
(1)试用 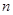 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率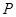 ;
;
(2)若 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(3)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为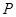 ,当
,当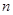 取多少时,
取多少时,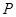 最大?
最大?
查看习题详情和答案>>
(本小题满分13分)
一个口袋中有2个白球和![]() 个红球(
个红球(![]() ,且
,且![]() ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖。
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖。
(1)试用含![]() 的代数式表示一次摸球中奖的概率P;
的代数式表示一次摸球中奖的概率P;
(2)若![]() ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为![]() ,当
,当![]() 为何值时,
为何值时,![]() 最大。
最大。
 个红球
个红球 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。 ;
; ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;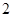 个白球和
个白球和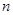 个红球
个红球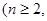 且
且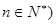 ,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.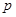 ;
;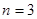 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;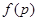 ,当
,当