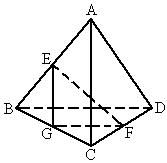
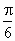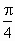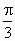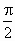摘要:并设.则...∵AC的中点为.
网址:http://m.1010jiajiao.com/timu_id_50428[举报]
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2| 3 |
(Ⅰ)求证SA⊥SC;
(Ⅱ)在平面几何中,推导三角形内切圆的半径公式r=
| 2S |
| l |
①以内切圆的圆心O为顶点,将三角形ABC分割成三个小三角形:△OAB,△OAC,△OB
 C.
C.②设△ABC三边长分别为a,b,c.由S△ABC=S△OBC+S△OAC+S△OAB,
得S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
类比上述方法,请给出四面体内切球半径的计算公式(不要求说明类比过程),并利用该公式求出三棱锥S-ABC内切球的半径. 查看习题详情和答案>>
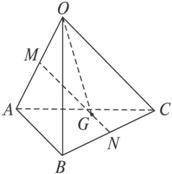
已知空间四边形OABC,如右图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且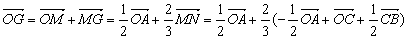 =2
=2 ,现用基向量
,现用基向量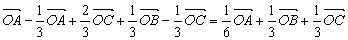 、
、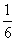 、
、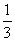 表示向量
表示向量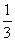 ,并设OG=x·
,并设OG=x·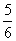 +y·
+y·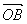 +z·
+z· ,则x、y、z的和为__________.
,则x、y、z的和为__________.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
A.[选修4-1:几何证明选讲]
已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与点A,C重合),延长BD至点E.
求证:AD的延长线平分∠CDE
B.[选修4-2:矩阵与变换]
已知矩阵
(1)求A的逆矩阵A-1;
(2)求A的特征值和特征向量.
C.[选修4-4:坐标系与参数方程]
已知曲线C的极坐标方程为ρ=4sinθ,以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,直线l的参数方程为 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.
D.[选修4-5,不等式选讲](本小题满分10分)
设a,b,c均为正实数,求证: .
.
 查看习题详情和答案>>
查看习题详情和答案>>
A.[选修4-1:几何证明选讲]
已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与点A,C重合),延长BD至点E.
求证:AD的延长线平分∠CDE
B.[选修4-2:矩阵与变换]
已知矩阵

(1)求A的逆矩阵A-1;
(2)求A的特征值和特征向量.
C.[选修4-4:坐标系与参数方程]
已知曲线C的极坐标方程为ρ=4sinθ,以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,直线l的参数方程为
 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.D.[选修4-5,不等式选讲](本小题满分10分)
设a,b,c均为正实数,求证:
 .
. 查看习题详情和答案>>
查看习题详情和答案>>
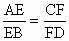 ,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于
,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于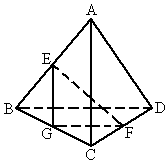
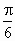
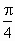
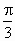
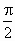
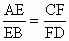 ,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于
,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于