网址：http://m.1010jiajiao.com/timu_id_502032[举报]
由所有既属于集合A又属于集合B的元素所成的集合，叫做A与B的________，记作A∩B，即A∩B＝{x|x∈A，且x∈B}．
可这样理解：交集A∩B是由两集合A与B的“公有”元素所组成的集合．用Venn图表示，如图．
易知：(1)若两集合A与B无公共关系，则A∩B＝________；
(2)A∩B________A，A∩B________B；
(3)A∩A＝________，A∩
＝________，A∩B＝B∩A；
(4)若A
B，则A∩B＝________；若A∩B＝A，则A________B；
(5)设U为全集，则A∩(
A)＝________．
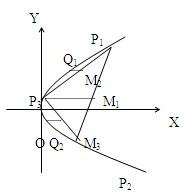已知抛物线y2=2x．（1）在抛物线上任取二点P1（x1，y1），P2（x2，y2），经过线段P1P2的中点作直线平行于抛物线的轴，和抛物线交于点P3，证明△P1P2P3的面积为
| 1 | 16 |
（2）经过线段P1P3、P2P3的中点分别作直线平行于抛物线的轴，与抛物线依次交于Q1、Q2，试将△P1P3Q1与△P2P3Q2的面积和用y1，y2表示出来；
（3）仿照（2）又可做出四个更小的三角形，如此继续下去可以做一系列的三角形，由此设法求出线段P1P2与抛物线所围成的图形的面积． 查看习题详情和答案>>
（1）当a=
| 1 |
| 3 |
（2）当a=
| 1 |
| 3 |
（3）若a＞0，函数f（x）在区间（m，n）上既有最大值又有最小值，请分别求出m，n的取值范围（用a表示）．
| y2 |
| m |
（1）由曲线C上任一点E向x轴作垂线，垂足为F，点P在
| EF |
| EP |
| 1 |
| 3 |
| PF |
（2）如果直线l的斜率为
| 2 |
| MA |
| MB |
| 9 |
| 2 |
已知数列
是各项均不为0的等差数列，公差为d，
为其前n项和，且满足
,
．数列
满足
,，
为数列的前n项和．
（1）求数列的通项公式
和数列的前n项和；
（2）若对任意的，不等式
恒成立，求实数
的取值范围；
（3）是否存在正整数
，使得
成等比数列？若存在，求出所有的值；若不存在，请说明理由．
【解析】第一问利用在
中，令n=1，n=2，
得
即
解得
，，
[
又时，
满足，
，
第二问，①当n为偶数时，要使不等式
恒成立，即需不等式
恒成立．
，等号在n=2时取得．
此时
需满足
．
②当n为奇数时，要使不等式恒成立，即需不等式
恒成立．
是随n的增大而增大， n=1时取得最小值-6．
此时 需满足
．
第三问
，
若
成等比数列，则
，
即． 
由，可得
，即
，
． 
（1）（法一）在中，令n=1，n=2，
得 即
解得，， [
又时，满足，
，
．
（2）①当n为偶数时，要使不等式恒成立，即需不等式恒成立．
，等号在n=2时取得．
此时 需满足．
②当n为奇数时，要使不等式恒成立，即需不等式恒成立．
是随n的增大而增大， n=1时取得最小值-6．
此时 需满足．
综合①、②可得的取值范围是．
（3），
若成等比数列，则，
即．
由，可得，即，
．
又
，且m>1，所以m=2，此时n=12．
因此，当且仅当m=2，
n=12时，数列
中的成等比数列
查看习题详情和答案>>