ЬтФПФкШн
 вбжЊХзЮяЯпy2=2xЃЎ
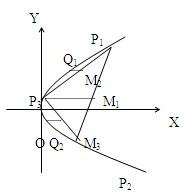
вбжЊХзЮяЯпy2=2xЃЎЃЈ1ЃЉдкХзЮяЯпЩЯШЮШЁЖўЕуP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌОЙ§ЯпЖЮP1P2ЕФжаЕузїжБЯпЦНаагкХзЮяЯпЕФжсЃЌКЭХзЮяЯпНЛгкЕуP3ЃЌжЄУїЁїP1P2P3ЕФУцЛ§ЮЊ
| 1 | 16 |
ЃЈ2ЃЉОЙ§ЯпЖЮP1P3ЁЂP2P3ЕФжаЕуЗжБ№зїжБЯпЦНаагкХзЮяЯпЕФжсЃЌгыХзЮяЯпвРДЮНЛгкQ1ЁЂQ2ЃЌЪдНЋЁїP1P3Q1гыЁїP2P3Q2ЕФУцЛ§КЭгУy1ЃЌy2БэЪОГіРДЃЛ
ЃЈ3ЃЉЗТееЃЈ2ЃЉгжПЩзіГіЫФИіИќаЁЕФШ§НЧаЮЃЌШчДЫМЬајЯТШЅПЩвдзівЛЯЕСаЕФШ§НЧаЮЃЌгЩДЫЩшЗЈЧѓГіЯпЖЮP1P2гыХзЮяЯпЫљЮЇГЩЕФЭМаЮЕФУцЛ§ЃЎ
ЗжЮіЃКЃЈ1ЃЉИљОнP1КЭP2ЕФзјБъПЩБэЪОГіP1P2ЕФжаЕуЕФзјБъЃЌНјЖјЧѓЕУP3ЕФКсзјБъКЭзнзјБъЃЎДњШыЁїP1P2P3ЕФУцЛ§БэДяЪНЃЌЛЏМђећРэМДПЩЃЎ
ЃЈ2ЃЉИљОнP1КЭP3ЕФзјБъПЩБэЪОГіP1P3ЕФжаЕуЕФзјБъЃЌПЩЧѓГіЕуQ1ЕФКсЁЂзнзјБъКЭЕуQ2ЕФКсЁЂзнзјБъЃЌдйгЩааСаЪНЧѓУцЛ§ЕФЗНЗЈЧѓГіУцЛ§ЃЎ
ЃЈ3ЃЉИљОнЯпЖЮP1P2гыХзЮяЯпЫљЮЇГЩЕФЭМаЮЕФУцЛ§ЕШгкSЁїp1p2p3 +ЃЈSЁїP1 Q2P3+sЁїp3Q2p2 ЃЉПЩЕУЕНД№АИЃЎ
ЃЈ2ЃЉИљОнP1КЭP3ЕФзјБъПЩБэЪОГіP1P3ЕФжаЕуЕФзјБъЃЌПЩЧѓГіЕуQ1ЕФКсЁЂзнзјБъКЭЕуQ2ЕФКсЁЂзнзјБъЃЌдйгЩааСаЪНЧѓУцЛ§ЕФЗНЗЈЧѓГіУцЛ§ЃЎ
ЃЈ3ЃЉИљОнЯпЖЮP1P2гыХзЮяЯпЫљЮЇГЩЕФЭМаЮЕФУцЛ§ЕШгкSЁїp1p2p3 +ЃЈSЁїP1 Q2P3+sЁїp3Q2p2 ЃЉПЩЕУЕНД№АИЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉЁпP1ЕФзјБъЮЊЃЈx1ЃЌy1ЃЉЃЌP2ЕФзјБъЮЊЃЈx2ЃЌy2ЃЉЃЌ
ЁрP1P2ЕФжаЕуЮЊM1(
ЃЌ
)
ЕуP3ЕФКсзјБъx=
=
ЃЌзнзјБъy=
ЁїP1P2P3ЕФУцЛ§=
ЕФОјЖджЕ
=
|x1y2-x2y1+
(y1+y2)+
(y1+y2)2|
=
|
-
+
(y1+y2)+
(y1+y2)2|
=
|y1-y2|•|4y1y2-2(y1+y2)2+(y1+y2)2|
=
|y1-y2|•|-(y1-y2)2|
=
|y1 -y2|3ЃЎ
ЃЈ2ЃЉЁпP1ЕФзјБъЮЊЃЈx1ЃЌy1ЃЉЃЌ
P3ЕФзјБъЮЊ(
ЃЌ
)ЃЌ
ЁрP1P3ЕФжаЕуЮЊM2(
ЃЌ
)ЃЌ
ЕуQ1ЕФКсзјБъx=
=
ЃЌзнзјБъy=
.
ЭЌРэЃЌЕуQ2ЕФКсзјБъx=
ЃЌзнзјБъy=
.
ЁїP1P3Q1ЕФУцЛ§+ЁїP2P3Q2ЕФУцЛ§
=
ЕФОјЖджЕ+
ЕФОјЖджЕ
=
|y22[2(y1+y2)-(3y1+y2)]+
[2(y1+y2)-(3y1+y2)]+
[(3y1+y2)2-4(y1+y2)2]|+
|y22[2(y1+y2)-(y1+3y2)]+
[2(y1+y2)-(y1+3y2)]+
[(y1+3y2)2-4(y1+y2)2]|
=
|y2-y1|•|(y1-y2)2|+
|y1-y2|•|ЃЈy2-y1ЃЉ2|
=
|y1-y2|3ЃЎ
ЃЈ3ЃЉЯпЖЮP1P2гыХзЮяЯпЫљЮЇГЩЕФЭМаЮЕФУцЛ§
S=SЁїp1p2p3 +ЃЈSЁїP1 Q2P3+sЁїp3Q2p2 ЃЉ
=
|y1-y2|3+
|y1-y2|3+
|y1-y2|3
=
=
|y1-y2|3ЃЎ
ЁрP1P2ЕФжаЕуЮЊM1(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
ЕуP3ЕФКсзјБъx=
| y2 |
| 2 |
| (y1+y2)2 |
| 8 |
| y1+y2 |
| 2 |
ЁїP1P2P3ЕФУцЛ§=
| 1 |
| 2 |
|
=
| 1 |
| 2 |
| x2-x1 |
| 2 |
| y1-y2 |
| 8 |
=
| 1 |
| 2 |
| y12y2 |
| 2 |
| y1y22 |
| 2 |
| y22-y12 |
| 2 |
| y1-y2 |
| 8 |
=
| 1 |
| 16 |
=
| 1 |
| 16 |
=
| 1 |
| 16 |
ЃЈ2ЃЉЁпP1ЕФзјБъЮЊЃЈx1ЃЌy1ЃЉЃЌ
P3ЕФзјБъЮЊ(
| (y1+y2)2 |
| 8 |
| y1+y2 |
| 2 |
ЁрP1P3ЕФжаЕуЮЊM2(
| 5y12+2y1y2+y22 |
| 16 |
| 3y1+y2 |
| 4 |
ЕуQ1ЕФКсзјБъx=
| y2 |
| 2 |
| (3y1+y2)2 |
| 32 |
| 3y1+y2 |
| 4 |
ЭЌРэЃЌЕуQ2ЕФКсзјБъx=
| (y1+3y2)2 |
| 32 |
| y1+3y2 |
| 4 |
ЁїP1P3Q1ЕФУцЛ§+ЁїP2P3Q2ЕФУцЛ§
=
| 1 |
| 2 |
|
| 1 |
| 2 |
|
=
| 1 |
| 16 |
| (y1+y2)(3y1+y2) |
| 8 |
| y2 |
| 4 |
| 1 |
| 16 |
| (y1+y2)(y1+3y2) |
| 8 |
| y2 |
| 4 |
=
| 1 |
| 128 |
| 1 |
| 128 |
=
| 1 |
| 64 |
ЃЈ3ЃЉЯпЖЮP1P2гыХзЮяЯпЫљЮЇГЩЕФЭМаЮЕФУцЛ§
S=SЁїp1p2p3 +ЃЈSЁїP1 Q2P3+sЁїp3Q2p2 ЃЉ
=
| 1 |
| 16 |
| 1 |
| 64 |
| 1 |
| 256 |
=
| ||
1-
|
| 1 |
| 12 |
ЕуЦРЃКБОЬтжївЊПМВщХзЮяЯпЕФЛљБОаджЪКЭгУааСаЪНЕФЗНЗЈЧѓУцЛ§ЃЎПМВщМЦЫуФмСІКЭзлКЯдЫгУФмСІЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
вбжЊХзЮяЯпy2=2xЃЌЩшЕуAЕФзјБъЮЊЃЈ
ЃЌ0ЃЉЃЌдђХзЮяЯпЩЯОрЕуAзюНќЕФЕуPЕФзјБъЮЊЃЈЁЁЁЁЃЉ
| 2 |
| 3 |
| AЁЂЃЈ0ЃЌ0ЃЉ |
| BЁЂЃЈ0ЃЌ1ЃЉ |
| CЁЂЃЈ1ЃЌ0ЃЉ |
| DЁЂЃЈ-2ЃЌ0ЃЉ |