摘要:设AC=BC=CC1=2a. AC⊥ BC
网址:http://m.1010jiajiao.com/timu_id_501922[举报]
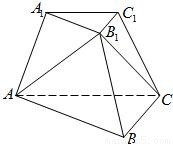
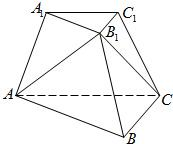 如图,已知三棱台ABC-A1B1C1,等边三角形AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.
如图,已知三棱台ABC-A1B1C1,等边三角形AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.(1)求点A到面B1BCC1的距离;
(2)求二面角A-B1B-C的余弦值;
(3)设
| AM |
| 2 |
| 5 |
| AB |
如图,已知三棱台ABC-A1B1C1,等边三角形AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.
(1)求点A到面B1BCC1的距离;
(2)求二面角A-B1B-C的余弦值;
(3)设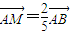 ,|MA1|=x,|CC1|=y,试将y表示为x的函数.
,|MA1|=x,|CC1|=y,试将y表示为x的函数.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求点A到面B1BCC1的距离;
(2)求二面角A-B1B-C的余弦值;
(3)设
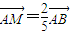 ,|MA1|=x,|CC1|=y,试将y表示为x的函数.
,|MA1|=x,|CC1|=y,试将y表示为x的函数. 查看习题详情和答案>>
查看习题详情和答案>>
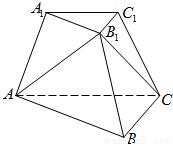
如图,已知三棱台ABC-A1B1C1,等边三角形AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.
(1)求点A到面B1BCC1的距离;
(2)求二面角A-B1B-C的余弦值;
(3)设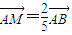 ,|MA1|=x,|CC1|=y,试将y表示为x的函数.
,|MA1|=x,|CC1|=y,试将y表示为x的函数.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求点A到面B1BCC1的距离;
(2)求二面角A-B1B-C的余弦值;
(3)设
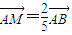 ,|MA1|=x,|CC1|=y,试将y表示为x的函数.
,|MA1|=x,|CC1|=y,试将y表示为x的函数. 查看习题详情和答案>>
查看习题详情和答案>>
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点,且 .
.
(Ⅰ)求证:CN∥平面AMB1;
(Ⅱ)求证: B1M⊥平面AMG.

【解析】本试题主要是考查了立体几何汇总线面的位置关系的运用。第一问中,要证CN∥平面AMB1;,只需要确定一条直线CN∥MP,既可以得到证明
第二问中,∵CC1⊥平面ABC,∴平面CC1 B1 B⊥平面ABC,得到线线垂直,B1M⊥AG,结合线面垂直的判定定理和性质定理,可以得证。
解:(Ⅰ)设AB1 的中点为P,连结NP、MP ………………1分


 ∵CM
∵CM  ,NP
,NP  ,∴CM
NP, …………2分
,∴CM
NP, …………2分
∴CNPM是平行四边形,∴CN∥MP …………………………3分
∵CN 平面AMB1,MP奂 平面AMB1,∴CN∥平面AMB1…4分
(Ⅱ)∵CC1⊥平面ABC,∴平面CC1 B1 B⊥平面ABC,
∵AG⊥BC,∴AG⊥平面CC1 B1 B,∴B1M⊥AG………………6分
∵CC1⊥平面ABC,平面A1B1C1∥平面ABC,∴CC1⊥AC,CC1⊥B1 C,
设:AC=2a,则
 …………………………8分
…………………………8分
同理, …………………………………9分
…………………………………9分
∵ BB1∥CC1,∴BB1⊥平面ABC,∴BB1⊥AB,

 ………………………………10分
………………………………10分

查看习题详情和答案>>