题目内容
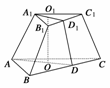
如图,已知三棱台ABC-A1B1C1,等边三角形AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.(1)求点A到面B1BCC1的距离;
(2)求二面角A-B1B-C的余弦值;
(3)设
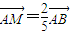 ,|MA1|=x,|CC1|=y,试将y表示为x的函数.
,|MA1|=x,|CC1|=y,试将y表示为x的函数.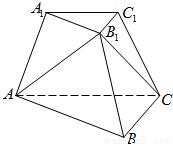
【答案】分析:(1)由题意因为面AB1C⊥面ABC,所以B1D⊥ABC,利用三棱锥的体积可以进行定点进行轮换的方法求解点到面的距离;
(2)由题意过D作DE∥BC,以D为原点,DE、DC、DB1所在直线为x轴、y轴、z轴建立空间直角坐标系,建立空间直角坐标系,先设出两个半平面的法向量的坐标,并利用法向量的定义解出坐标,在利用平面法向量的夹角求出二面角;
(3)设B1C1=m,则A1C1=2m,有上两问写出一些点的坐标,利用两点间的距离公式求出两点间的距离.
解答:解:(1)作B1D⊥AC,垂足为D,因为面AB1C⊥面ABC,
所以B1D⊥ABC,因为∠ACB=90o所以BC⊥AB1C.设A到面B1BCC1的距离为h,由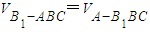 ,
,
即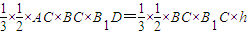 ,解得
,解得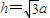 .
.
(2)过D作DE∥BC,以D为原点,DE、DC、DB1所在直线为x轴、y轴、z轴建立空间直角坐标系,则A(0,-a,0)、B(a,a,0)、C(0,a,0)、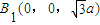 ,设平面AB1B的一个法向量为
,设平面AB1B的一个法向量为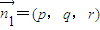 ,则
,则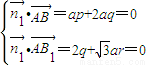 ,取r=1得
,取r=1得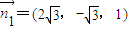 ,同理,平面B1BC的一个法向量
,同理,平面B1BC的一个法向量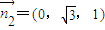 ,
,
所以二面角A-B1B-C的余弦值为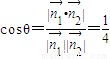 .
.
(3)设B1C1=m,则A1C1=2m,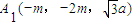 ,
,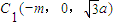 ,由
,由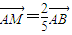 得
得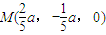 ,根据空间两点的距离公式,
,根据空间两点的距离公式,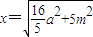 ,
, ,
,
所以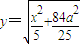 .
.
点评:(1)是等体积法求点到平面的距离;(2)是在一个非长方体中建立空间直角坐标系求二面角的余弦值;(3)是确定一些空间点的坐标,求空间两点的距离.
(2)由题意过D作DE∥BC,以D为原点,DE、DC、DB1所在直线为x轴、y轴、z轴建立空间直角坐标系,建立空间直角坐标系,先设出两个半平面的法向量的坐标,并利用法向量的定义解出坐标,在利用平面法向量的夹角求出二面角;
(3)设B1C1=m,则A1C1=2m,有上两问写出一些点的坐标,利用两点间的距离公式求出两点间的距离.
解答:解:(1)作B1D⊥AC,垂足为D,因为面AB1C⊥面ABC,
所以B1D⊥ABC,因为∠ACB=90o所以BC⊥AB1C.设A到面B1BCC1的距离为h,由
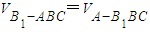 ,
,即
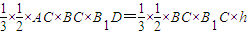 ,解得
,解得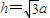 .
.(2)过D作DE∥BC,以D为原点,DE、DC、DB1所在直线为x轴、y轴、z轴建立空间直角坐标系,则A(0,-a,0)、B(a,a,0)、C(0,a,0)、
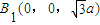 ,设平面AB1B的一个法向量为
,设平面AB1B的一个法向量为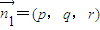 ,则
,则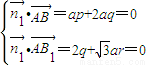 ,取r=1得
,取r=1得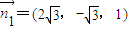 ,同理,平面B1BC的一个法向量
,同理,平面B1BC的一个法向量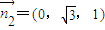 ,
,所以二面角A-B1B-C的余弦值为
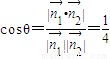 .
.(3)设B1C1=m,则A1C1=2m,
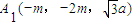 ,
,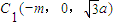 ,由
,由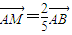 得
得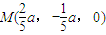 ,根据空间两点的距离公式,
,根据空间两点的距离公式,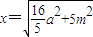 ,
, ,
,所以
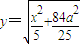 .
.点评:(1)是等体积法求点到平面的距离;(2)是在一个非长方体中建立空间直角坐标系求二面角的余弦值;(3)是确定一些空间点的坐标,求空间两点的距离.

练习册系列答案
相关题目